题目内容
7．已知定义在R上函数f（x）=$\left\{\begin{array}{l}{x^2}，x∈[{0，1}）\\-{x^2}，x∈[{-1，0}）\end{array}$，且f（x+2）=f（x），g（x）=$\frac{1}{x-2}$，则方程f（x）=g（x）在区间[-3，7]上的所有实根之和为（ ）| A． | 9 | B． | 10 | C． | 11 | D． | 12 |
分析 由f（x+2）=f（x），得到函数是周期为2的周期函数，分别作出函数f（x），g（x）在[-3，7]上的图象，利用图象观察交点的个数和规律，然后进行求解．
解答 解：∵f（x+2）=f（x），
∴函数f（x）是周期为2的周期函数，
∵g（x）=$\frac{1}{x-2}$，
∴g（x）关于直线x=2对称．
分别作出函数f（x），g（x）在[-3，7]上的图象，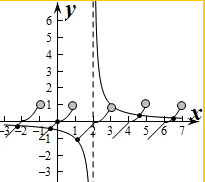
由图象可知两个函数的交点个数为6个，设6个交点的横坐标从小到大为x1，x2，x3，x4，x5，x6，
且这6个交点接近点（2，0）对称，
则$\frac{{x}_{1}+{x}_{6}}{2}$=2，即x1+x6=4，
所以x1+x2+x3+x4+x5+x6=3（x1+x6）=3×4=12，
其中x=3时，不成立，则f（x）=g（x）在区间[-3，7]上的所有实根之和为12-3=9，
故选：A．
点评 本题主要考查函数交点个数和取值的判断，利用数形结合是解决此类问题的基本方法．本题综合性较强，难度较大
练习册系列答案
课时训练江苏人民出版社系列答案
黄冈经典趣味课堂系列答案
启东小题作业本系列答案
相关题目
15．已知数列{an}满足${a_{n+1}}+{a_n}=（n+1）•cos\frac{nπ}{2}（n≥2，n∈{N^*}）$，Sn是数列{an}的前n项和，若S2017+m=1010，且a1•m＞0，则$\frac{1}{a_1}+\frac{1}{m}$的最小值为（ ）
| A． | 2 | B． | $\sqrt{2}$ | C． | $2\sqrt{2}$ | D． | $2+\sqrt{2}$ |
16．已知$\frac{{\sqrt{2}}}{2}（{sin\frac{α}{2}-cos\frac{α}{2}}）=\frac{{\sqrt{6}}}{3}$，则sinα的值为（ ）
| A． | $-\frac{1}{3}$ | B． | $\frac{1}{3}$ | C． | $\frac{{2\sqrt{2}}}{3}$ | D． | $-\frac{{2\sqrt{2}}}{3}$ |