题目内容
6.△ABC的内角A,B,C的对边分别为a,b,c,若$A=45°,a=\sqrt{2},b=\sqrt{3}$,则B等于( )| A. | 30° | B. | 60° | C. | 30°或150° | D. | 60°或120° |
分析 由已知利用正弦定理可求sinB的值,结合B的范围,由特殊角的三角函数值即可得解.
解答 解:∵$A=45°,a=\sqrt{2},b=\sqrt{3}$,
∴由正弦定理可得:sinB=$\frac{bsinA}{a}$=$\frac{\sqrt{3}×\frac{\sqrt{2}}{2}}{\sqrt{2}}$=$\frac{\sqrt{3}}{2}$,
∵B∈(0°,180°),
∴B=60°,或120°.
故选:D.
点评 本题主要考查了正弦定理,特殊角的三角函数值在解三角形中的应用,考查了转化思想,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.已知$\frac{{\sqrt{2}}}{2}({sin\frac{α}{2}-cos\frac{α}{2}})=\frac{{\sqrt{6}}}{3}$,则sinα的值为( )
| A. | $-\frac{1}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{{2\sqrt{2}}}{3}$ | D. | $-\frac{{2\sqrt{2}}}{3}$ |
1.已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{{\sqrt{2}}}{2}$,双曲线 x2-y2=1的渐近线与椭圆C有四个交点,以这四个交点为顶点的四边形的面积为8,则椭圆C的方程为( )
| A. | $\frac{{x}^{2}}{8}$+$\frac{{y}^{2}}{2}$=1 | B. | $\frac{{x}^{2}}{12}$+$\frac{{y}^{2}}{6}$=1 | C. | $\frac{{x}^{2}}{6}$+$\frac{{y}^{2}}{3}$=1 | D. | $\frac{{x}^{2}}{20}$+$\frac{{y}^{2}}{5}$=1 |
18.为了响应厦门市政府“低碳生活,绿色出行”的号召,思明区委文明办率先全市发起“少开一天车,呵护厦门蓝”绿色出行活动,“从今天开始,从我做起,力争每周至少一天不开车,上下班或公务活动带头选择步行、骑车或乘坐公交车,鼓励拼车…”铿锵有力的话语,传递了低碳生活、绿色出行的理念.某机构随机调查了本市500名成年市民某月的骑车次数,统计如下:
联合国世界卫生组织于2013年确定新的年龄分段:44岁及以下为青年人,45岁至59岁为中年人,60岁及以上为老年人.记本市一个年满18岁的青年人月骑车的平均次数为μ.以样本估计总体.
(Ⅰ)估计μ的值;
(Ⅱ)在本市老年人或中年人中随机访问3位,其中月骑车次数超过μ的人数记为ξ,求ξ的分布列与数学期望.
 | [0,10) | [10,20) | [20,30) | [30,40) | [40,50) | [50,60] |
| 18岁至30岁 | 6 | 14 | 20 | 32 | 40 | 48 |
| 31岁至44岁 | 4 | 6 | 20 | 28 | 40 | 42 |
| 45岁至59岁 | 22 | 18 | 33 | 37 | 19 | 11 |
| 60岁及以上 | 15 | 13 | 10 | 12 | 5 | 5 |
(Ⅰ)估计μ的值;
(Ⅱ)在本市老年人或中年人中随机访问3位,其中月骑车次数超过μ的人数记为ξ,求ξ的分布列与数学期望.
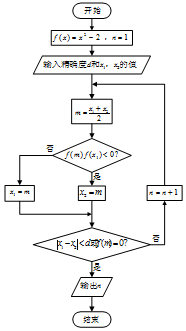 二分法是求方程近似解的一种方法,其原理是“一分为二,无限逼近”.执行如图所示的程序框图,若输入x1=1,x2=2,d=0.1,则输出n的值为( )
二分法是求方程近似解的一种方法,其原理是“一分为二,无限逼近”.执行如图所示的程序框图,若输入x1=1,x2=2,d=0.1,则输出n的值为( )