题目内容
4．
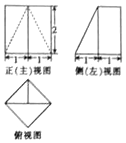已知一个几何体的三视图如图所示，则该几何体的体积为（ ）| A． | $\frac{32}{3}$ | B． | $\frac{16}{3}$ | C． | $\frac{8}{3}$ | D． | $\frac{4}{3}$ |
分析 根据几何体的三视图知该几何体是等底同高的三棱锥与三棱柱的组合体，
结合图中数据即可求出它的体积．
解答 解：根据几何体的三视图知，
该几何体是等底同高的三棱锥与三棱柱的组合体，
画出直观图如图所示；
则几何体的体积为
V几何体=V三棱柱+V三棱锥
=$\frac{1}{2}$×${（\sqrt{2}）}^{2}$×2+$\frac{1}{3}$×$\frac{1}{2}$×${（\sqrt{2}）}^{2}$×2
=$\frac{8}{3}$．
故选：C．
点评 本题考查了空间几何体三视图的应用问题，是基础题目．
练习册系列答案
相关题目
15．已知数列{an}满足${a_{n+1}}+{a_n}=（n+1）•cos\frac{nπ}{2}（n≥2，n∈{N^*}）$，Sn是数列{an}的前n项和，若S2017+m=1010，且a1•m＞0，则$\frac{1}{a_1}+\frac{1}{m}$的最小值为（ ）
| A． | 2 | B． | $\sqrt{2}$ | C． | $2\sqrt{2}$ | D． | $2+\sqrt{2}$ |
16．已知$\frac{{\sqrt{2}}}{2}（{sin\frac{α}{2}-cos\frac{α}{2}}）=\frac{{\sqrt{6}}}{3}$，则sinα的值为（ ）
| A． | $-\frac{1}{3}$ | B． | $\frac{1}{3}$ | C． | $\frac{{2\sqrt{2}}}{3}$ | D． | $-\frac{{2\sqrt{2}}}{3}$ |