题目内容
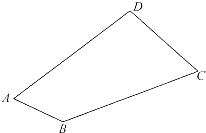如图，在四边形ABCD中，若∠A=∠C=60°，AD=BC=2，且AB≠CD，则四边形ABCD的面积为（ ）A、
| ||||
B、
| ||||
C、
| ||||
| D、与点B的位置有关 |
考点：余弦定理,正弦定理
专题：解三角形
分析：连接BD，分别在△ABD和△BCD中表示出BD，建立等式求得AB+CD的值，最后根据三角形面积公式求得答案．
解答：
解：连接BD，
在△ABD中，BD=
=
，
在△BCD中，BD=
，
∴4+AB2-2AB=4+CD2-2CD，
整理得（AB+CD-2）（AB-CD）=0，
∵AB≠CD，
∴AB+CD=2，
∴SABCD=S△BCD+S△ABD=
AD•ABsinA+
•BC•CDsinC=
•2•
（AB+CD）=
，
故答案为：
在△ABD中，BD=
| AD2+AB2-2AD•AB•cosA |
| 4+AB2-2AB |
在△BCD中，BD=
| 4+CD2-2CD |
∴4+AB2-2AB=4+CD2-2CD，
整理得（AB+CD-2）（AB-CD）=0，
∵AB≠CD，
∴AB+CD=2，
∴SABCD=S△BCD+S△ABD=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 3 |
故答案为：
| 3 |
点评：本题主要考查了正弦定理的应用．解本题的关键时求出AB+CD的值．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
设α，β是方程x2-8x+k2=0的两根，且α，αβ，β成等差数列，则k=（ ）
| A、2 | B、4 | C、±2 | D、±4 |
不等式-x2+x+2≥0的解集是（ ）
| A、[-1，2] |
| B、（-∞，-1]∪[2，+∞） |
| C、[-2，1] |
| D、（-∞，-2]∪[1，+∞） |
若
=
，则cosα+sinα=（ ）
| cos2α | ||
cos(
|
| 1 |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知集合A={-1，0，1，2}，B={x|ln（x-1）=0}，则A∩B=（ ）
| A、{-1} | B、{0} |
| C、{1} | D、{2} |
设实数x，y满足
则z=
的取值范围是（ ）
|
| 2x+y+2 |
| x+1 |
A、[
| ||
B、[
| ||
C、[1，
| ||
| D、[1，3] |
已知函数f（x）=2sin（ωx+φ）（ω＞0，|φ|＜
）的部分图象如图所示，则（ ）
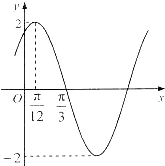
| π |
| 2 |
A、ω=2，φ=
| ||||
B、ω=
| ||||
C、ω=2，φ=
| ||||
D、ω=
|
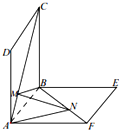如图正方形ABCD、ABEF的边长都是1，而且平面ABCD、ABEF互相垂直．点M在AC上移动，点N在BF上移动，若CM=BN=a（0＜a＜