题目内容
定义域为R的函数f(x)满足f(x+2)=2f(x),当x∈[0,2]时,f(x)=
若x∈[4,6]时,f(x)≥t2-2t-4恒成立,则实数t的取值范围是( )
|
A、[-
| ||||
B、[1-
| ||||
| C、[-1,3] | ||||
| D、[0,2] |
考点:函数恒成立问题
专题:函数的性质及应用
分析:先确定当x∈[0,2]时,f(x)的最小值为-
,利用函数f(x)满足f(x+2)=2f(x),可得x∈[4,6]时,f(x)的最小值为-1,从而可得-1≥t2-2t-4,即可得出结论.
| 1 |
| 4 |
解答:
解:当x∈[0,1)时,f(x)=x2-x∈[-
,0]
当x∈[1,2]时,f(x)=(x-2)x∈[-
,0]
∴当x∈[0,2]时,f(x)的最小值为-
,
又∵函数f(x)满足f(x+2)=2f(x),
当x∈[2,4]时,f(x)的最小值为-
,
当x∈[4,6]时,f(x)的最小值为-1,
∵x∈[4,6]时,f(x)≥t2-2t-4恒成立,
∴-1≥t2-2t-4
∴(t+1)(t-3)≤0,
解得:-1≤t≤3,
故选:C
| 1 |
| 4 |
当x∈[1,2]时,f(x)=(x-2)x∈[-
| 1 |
| 10 |
∴当x∈[0,2]时,f(x)的最小值为-
| 1 |
| 4 |
又∵函数f(x)满足f(x+2)=2f(x),
当x∈[2,4]时,f(x)的最小值为-
| 1 |
| 2 |
当x∈[4,6]时,f(x)的最小值为-1,
∵x∈[4,6]时,f(x)≥t2-2t-4恒成立,
∴-1≥t2-2t-4
∴(t+1)(t-3)≤0,
解得:-1≤t≤3,
故选:C
点评:本题考查的知识点是函数恒成立问题,考查函数的最值,是函数、不等式的综合应用,确定-1≥t2-2t-4是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
执行如图所示的程序框图,输出的k的值为( )


| A、2 | B、3 | C、4 | D、1 |
在同一直角坐标系中,函数f(x)=logax(a>0,a≠1)与函数g(x)=ax(a>0,a≠1)的图象可能是( )
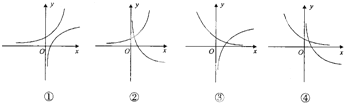

| A、①② | B、①③ | C、①④ | D、②④ |
在△ABC中,若AB=
,C=150°,则它的外接圆的面积为( )
| 3 |
| A、π | B、2π | C、3π | D、4π |