题目内容
已知函数f(x)=x2+mx+n,且函数f(x)的图象关于直线x=2对称.
(1)求实数m的值;
(2)设g(x)=2sin(
+
),若对任意x1,x2∈[-1,1].f(x2)<g(x1)恒成立,求n的取值范围;
(3)讨论方程[f(x)-n]=2n+1的实根个数.
(1)求实数m的值;
(2)设g(x)=2sin(
| πx |
| 6 |
| π |
| 3 |
(3)讨论方程[f(x)-n]=2n+1的实根个数.
考点:函数恒成立问题,二次函数的性质
专题:函数的性质及应用
分析:(1)由函数f(x)的图象关于直线x=2对称,得-
=2,求出即可;
(2)由(1)得:f(x)=(x-2)2+n-4,问题转化为对任意x1,x2∈[-1,1],f(x2)max<g(x1)min恒成立,求出f(x)max,g(x)min,从而问题解决;
3)方程[f(x)-n]=2n+1可化为|x2-4x|=2n+1,画出函数h(x)=|x2-4x|,通过讨论2n+1的范围,进而得到根的个数.
| m |
| 2 |
(2)由(1)得:f(x)=(x-2)2+n-4,问题转化为对任意x1,x2∈[-1,1],f(x2)max<g(x1)min恒成立,求出f(x)max,g(x)min,从而问题解决;
3)方程[f(x)-n]=2n+1可化为|x2-4x|=2n+1,画出函数h(x)=|x2-4x|,通过讨论2n+1的范围,进而得到根的个数.
解答:
解:(1)∵函数f(x)的图象关于直线x=2对称,
∴-
=2,即m=-4;
(2)由(1)得:f(x)=(x-2)2+n-4,
∵对任意x1,x2∈[-1,1].f(x2)<g(x1)恒成立,
∴x1,x2∈[-1,1]时,f(x2)max<g(x1)min恒成立,
又∵f(x)在[-1,1]递减,g(x)在[-1,1]递增,
∴x1,x2∈[-1,1]时:
f(x)max=f(-1)=n+5,g(x)min=g(-1)=1,
∴n+5<1,
∴n<-4;
(3)方程[f(x)-n]=2n+1可化为|x2-4x|=2n+1,
令h(x)=|x2-4x|,画出函数图象:
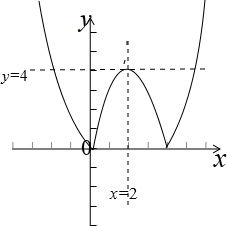 ,
,
∴当2n+1<0,即n<-
时,方程无实根,
当2n+1=0,即n=-
时,方程有2个实根,
当2n+1>4,即n>
时,方程有2个实根,
当2n+1=4,即n=
时,方程有3个实根,
当0<2n+1<4,即-
<n<
时,方程有4个实根.
∴-
| m |
| 2 |
(2)由(1)得:f(x)=(x-2)2+n-4,
∵对任意x1,x2∈[-1,1].f(x2)<g(x1)恒成立,
∴x1,x2∈[-1,1]时,f(x2)max<g(x1)min恒成立,
又∵f(x)在[-1,1]递减,g(x)在[-1,1]递增,
∴x1,x2∈[-1,1]时:
f(x)max=f(-1)=n+5,g(x)min=g(-1)=1,
∴n+5<1,
∴n<-4;
(3)方程[f(x)-n]=2n+1可化为|x2-4x|=2n+1,
令h(x)=|x2-4x|,画出函数图象:
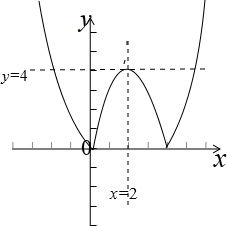 ,
,∴当2n+1<0,即n<-
| 1 |
| 2 |
当2n+1=0,即n=-
| 1 |
| 2 |
当2n+1>4,即n>
| 3 |
| 2 |
当2n+1=4,即n=
| 3 |
| 2 |
当0<2n+1<4,即-
| 1 |
| 2 |
| 3 |
| 2 |
点评:本题考查了二次函数的性质,考查函数恒成立问题,考查分类讨论思想,本题属于中档题.

练习册系列答案
相关题目
有600名同学参加夏令营,随机编号为000,001,…,599,现欲抽取50的样本,已知编号000~299的同学在第一营区,300~494的同学在第二营区,495-599的同学在第三营区,用系统抽样法,已知随机抽得的号码为002,则应从三个营区分别抽到的人数是( )
| A、26,16,8 |
| B、25,17,8 |
| C、25,16,9 |
| D、24,17,9 |
直线y=x+a与圆x2+y2=4交于点A、B,若
•
=-2(O为坐标原点),则实数a的为( )
| OA |
| OB |
A、
| ||||
B、
| ||||
C、
| ||||
| D、1 |
在等差数列{an}中,a1=3,a3=6则a5的值为( )
| A、15 | B、6 | C、81 | D、9 |
在△ABC中,已知sin2B-sin2C-sin2A=sinAsinC,则角B的大小为( )
| A、150° | B、30° |
| C、120° | D、60° |