题目内容
17.如果函数y=b与函数y=x2-3|x-1|-4x-3的图象恰好有三个交点,则b=$-6或-\frac{25}{4}$.分析 按x≥1和x<1分别去绝对值,得到分段函数,确定两函数图象的交点坐标,顶点坐标,结合分段函数的自变量取值范围求出符合条件的b的值.
解答 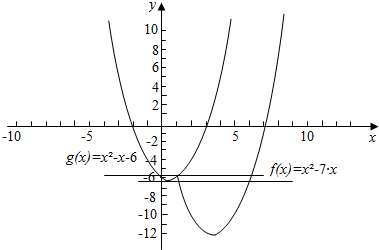 解:当x≥1时,函数y=x2-7x
解:当x≥1时,函数y=x2-7x
图象的一个端点为(1,-6),顶点坐标为$(\frac{7}{2},-\frac{49}{4})$,
当x<1时,函数y=x2-x-6.
顶点坐标为$(\frac{1}{2},-\frac{25}{4})$,
∴当b=-6或$b=-\frac{25}{4}$时,两图象恰有三个交点.
故答案为:$-6或-\frac{25}{4}$.
点评 本题考查了分段的两个二次函数的性质,根据绝对值里式子的符号分类,得到两个二次函数是解题的关键.

练习册系列答案
相关题目
5.已知几何体的三视图如图,则这个几何体自上而下依次是( )


| A. | 四棱台,圆台 | B. | 四棱台,四棱台 | C. | 四棱柱,四棱柱 | D. | 不能判断 |
2.已知函数f(x)=ex-mx+1的图象是曲线C,若曲线C不存在与直线y=ex垂直的切线,则实数m的取值范围是( )
| A. | (-∞,-$\frac{1}{e}$) | B. | [$\frac{1}{e}$,+∞) | C. | (-∞,$\frac{1}{e}$) | D. | (-∞,$\frac{1}{e}$] |
6.设全集U={a,b,c,d,e},集合A={a,b,c,d},B={c,d,e},则集合∁U(A∩B)=( )
| A. | {d} | B. | {a,b} | C. | {b,c,d} | D. | {a,b,e} |