题目内容
2.已知函数f(x)=ex-mx+1的图象是曲线C,若曲线C不存在与直线y=ex垂直的切线,则实数m的取值范围是( )| A. | (-∞,-$\frac{1}{e}$) | B. | [$\frac{1}{e}$,+∞) | C. | (-∞,$\frac{1}{e}$) | D. | (-∞,$\frac{1}{e}$] |
分析 求出函数的导数,设切点为(s,t),求得切线的斜率,若曲线C不存在与直线y=ex垂直的切线,则关于s的方程es-m=-$\frac{1}{e}$无实数解,由指数函数的值域,即可得到m的范围.
解答 解:函数f(x)=ex-mx+1的导数为f′(x)=ex-m,
设切点为(s,t),即有切线的斜率为es-m,
若曲线C不存在与直线y=ex垂直的切线,
则关于s的方程es-m=-$\frac{1}{e}$无实数解,
由于es>0,即有m-$\frac{1}{e}$≤0,
解得m≤$\frac{1}{e}$.
故选:D.
点评 本题考查导数的几何意义:函数在某点处的导数即为曲线在该点处的切线的斜率,同时考查两直线垂直的条件,运用指数函数的值域是解题的关键.

练习册系列答案
相关题目
8.下列函数中,既不是奇函数,也不是偶函数的是( )
| A. | f(x)=$\frac{1}{1+{x}^{2}}$ | B. | f(x)=x2+x | C. | f(x)=cos$\frac{x}{3}$ | D. | f(x)=$\frac{2}{x}$ |
10.已知某几何体的三视图的侧视图是一个正三角形,如图所示,则该几何体的体积等于( )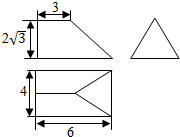

| A. | 12$\sqrt{3}$ | B. | 16$\sqrt{3}$ | C. | 20$\sqrt{3}$ | D. | 32$\sqrt{3}$ |
7.函数f(x)=Asin(ωx+$\frac{π}{6}$)(A>0,ω>0)的图象与x轴的交点的横坐标构成一个公差为$\frac{π}{2}$的等差数列,要得到函数g(x)=Acosωx的图象,只需将f(x)的图象( )
| A. | 向左平移$\frac{π}{6}$个单位 | B. | 向右平移$\frac{π}{3}$个单位 | ||
| C. | 向左平移$\frac{2π}{3}$个单位 | D. | 向右平移$\frac{2π}{3}$个单位 |