题目内容
11.已知椭圆方程为 $\frac{x^2}{4}+\frac{y^2}{3}$=1,P为椭圆上动点,Q(4,0)是X轴上的定点,M是PQ的中点,当点P在椭圆上运动时(1)写出该椭圆的参数方程
(2)求M的轨迹的参数方程.
分析 (1)由椭圆方程为 $\frac{x^2}{4}+\frac{y^2}{3}$=1,利用平方关系可得参数方程.
(2)设M(x,y),M是PQ的中点,则P(2x-4,2y).代入椭圆方程可得:(x-2)2+$\frac{4{y}^{2}}{3}$=1.利用平方关系即可得出.
解答 解:(1)由椭圆方程为 $\frac{x^2}{4}+\frac{y^2}{3}$=1,令$\left\{\begin{array}{l}{x=2cosθ}\\{y=\sqrt{3}sinθ}\end{array}\right.$(θ为参数).
(2)设M(x,y),M是PQ的中点,则P(2x-4,2y).
代入椭圆方程可得:$\frac{(2x-4)^{2}}{4}$+$\frac{4{y}^{2}}{3}$=1,化为(x-2)2+$\frac{4{y}^{2}}{3}$=1.
令x-2=cosα,$\frac{2y}{\sqrt{3}}$=sinα,可得$\left\{\begin{array}{l}{x=2+cosα}\\{y=\frac{\sqrt{3}}{2}sinα}\end{array}\right.$(α为参数).
点评 本题考查了椭圆的标准方程与参数方程、三角函数基本关系式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
18.已知a,b,a+b成等差数列,a,b,ab成等比数列,且$0<10{log_m}^{({ab})}<1$,则m的取值范围是( )
| A. | m>1 | B. | 1<m<8 | C. | m>8 | D. | 0<m<1或 m>8 |
16.已知定义在R上的奇函数f(x)满足f(x)=f(x+2),当x∈(0,1]时,f(x)=$\sqrt{x},则f(\frac{7}{2})$等于( )
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $-\frac{1}{2}$ | D. | $-\frac{{\sqrt{2}}}{2}$ |
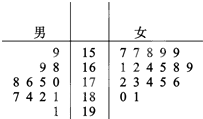 某部队为了在大阅兵中树立军队的良好形象,决定从参训的12名男兵和18名女兵中挑选出正式阅兵人员,这30名军人的身高如图:单位:cm
某部队为了在大阅兵中树立军队的良好形象,决定从参训的12名男兵和18名女兵中挑选出正式阅兵人员,这30名军人的身高如图:单位:cm