题目内容
3.已知实数x,y,z为正数,则$\frac{xy+yz}{{{x^2}+{y^2}+{z^2}}}$的最大值为$\frac{\sqrt{2}}{2}$.分析 实数x,y,z为正数,则$\frac{xy+yz}{{{x^2}+{y^2}+{z^2}}}$=$\frac{\frac{x}{y}+\frac{z}{y}}{(\frac{x}{y})^{2}+1+(\frac{z}{y})^{2}}$,令$\frac{x}{y}$=a>0,$\frac{z}{y}$=b>0,a+b=t>0.则$\frac{xy+yz}{{{x^2}+{y^2}+{z^2}}}$=$\frac{a+b}{{a}^{2}+{b}^{2}+1}$≤$\frac{a+b}{\frac{(a+b)^{2}}{2}+1}$=$\frac{t}{\frac{{t}^{2}}{2}+1}$=$\frac{1}{\frac{t}{2}+\frac{1}{t}}$,再利用基本不等式的性质即可得出.
解答 解:∵实数x,y,z为正数,则$\frac{xy+yz}{{{x^2}+{y^2}+{z^2}}}$=$\frac{\frac{x}{y}+\frac{z}{y}}{(\frac{x}{y})^{2}+1+(\frac{z}{y})^{2}}$,
令$\frac{x}{y}$=a>0,$\frac{z}{y}$=b>0,a+b=t>0.
则$\frac{xy+yz}{{{x^2}+{y^2}+{z^2}}}$=$\frac{a+b}{{a}^{2}+{b}^{2}+1}$≤$\frac{a+b}{\frac{(a+b)^{2}}{2}+1}$=$\frac{t}{\frac{{t}^{2}}{2}+1}$=$\frac{1}{\frac{t}{2}+\frac{1}{t}}$≤$\frac{1}{2\sqrt{\frac{t}{2}×\frac{1}{t}}}$=$\frac{\sqrt{2}}{2}$,当且仅当t=$\sqrt{2}$,即a=b=$\frac{\sqrt{2}}{2}$,即$\frac{x}{y}$=$\frac{z}{y}$=$\frac{\sqrt{2}}{2}$时取等号.
故答案为:$\frac{\sqrt{2}}{2}$.
点评 本题考查了换元法、基本不等式的性质,考查了推理能力与计算能力,属于难题.

 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案| A. | -1+2i | B. | -1-2i | C. | 1-2i | D. | 1+2i |
| A. | 200 | B. | 100 | C. | 90 | D. | 70 |
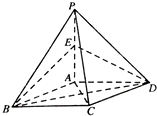 如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,且PA⊥底面ABCD,BD⊥PC,E是PA的中点,∠BAD=120°.
如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,且PA⊥底面ABCD,BD⊥PC,E是PA的中点,∠BAD=120°.