题目内容
已知命题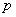 :“函数
:“函数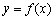 的图像关于点
的图像关于点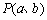 成中心对称图形”的充要条件为“函数
成中心对称图形”的充要条件为“函数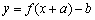 是奇函数”.
是奇函数”.
(1)试判断命题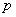 的真假?并说明理由;
的真假?并说明理由;
(2)设函数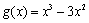 ,求函数
,求函数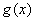 图像对称中心的坐标;
图像对称中心的坐标;
(3)试判断“存在实数a和b,使得函数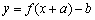 是偶函数”是“函数
是偶函数”是“函数 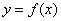 的图像关于某直线成轴对称图像”成立的什么条件?请说明理由.
的图像关于某直线成轴对称图像”成立的什么条件?请说明理由.
解:
(1)命题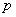 为真命题;
为真命题;
充分性:若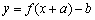 为奇函数,则
为奇函数,则
即
设 为
为 图像上任一点,则
图像上任一点,则 关于
关于 的对称点为
的对称点为

 在
在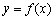 图像上,即
图像上,即 的图像上,即
的图像上,即 的图像关于
的图像关于 对称
对称
必要性:若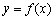 的图像关于
的图像关于
设 为
为 图像上任一点,则由上知:
图像上任一点,则由上知:
令 取
取 ,则
,则
即
 为奇函数
为奇函数
综上命题为真
(2)设函数 为奇函数,
为奇函数,
则

∵ 为奇函数,则
为奇函数,则 ,即
,即
由命题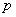 为真命题,则函数
为真命题,则函数 的图像对称中心为
的图像对称中心为
(3)ⅰ.当 时“存在实数
时“存在实数 和
和 ,使得函数
,使得函数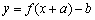 是偶函数”是“函数
是偶函数”是“函数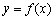 的图像关于直线
的图像关于直线 成轴对称图形”的充要条件;(证明方法参考(1))
成轴对称图形”的充要条件;(证明方法参考(1))
ⅱ. 当 不为
不为 时“存在实数
时“存在实数 和
和 ,使得函数
,使得函数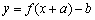 是偶函数”是“函数
是偶函数”是“函数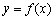 的图像关于直线
的图像关于直线 成轴对称图形”的充分不必要条件
成轴对称图形”的充分不必要条件

练习册系列答案
相关题目
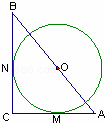
 的边长为
的边长为 ,记以
,记以 为起点,其余顶点为终点的向量分别为
为起点,其余顶点为终点的向量分别为 ,
, ,
, .若
.若 且
且 ,则
,则 的所有可能取值为
的所有可能取值为  上的函数
上的函数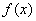 ,满足
,满足 ,若
,若 时
时
 ,则
,则 .
. 当
当 ,
, ,若在区间
,若在区间 内,函数
内,函数 有三个不同零点,则实数a的取值范围是 .
有三个不同零点,则实数a的取值范围是 .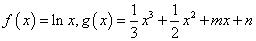 ,直线
,直线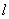 与函数
与函数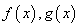 的图象都相切于点
的图象都相切于点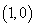
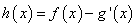 (其中
(其中 是
是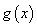 的导函数),求函数
的导函数),求函数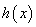 的值域.
的值域. 的解集为
的解集为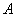 ,且
,且 .
.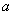 的值;
的值; 的最小值.
的最小值.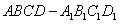 中,侧面
中,侧面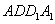 ⊥底面
⊥底面 ,
, ,底面
,底面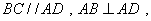
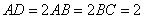 ,O为
,O为 中点。
中点。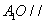 平面
平面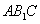 ;
;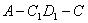 的余弦值.
的余弦值.