题目内容
已知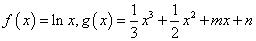 ,直线
,直线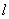 与函数
与函数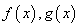 的图象都相切于点
的图象都相切于点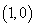
(1)求直线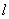 的方程及
的方程及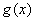 的解析式;
的解析式;
(2)若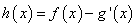 (其中
(其中 是
是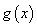 的导函数),求函数
的导函数),求函数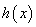 的值域.
的值域.
解:(1)直线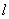 是函数
是函数 在点
在点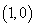 处的切线,故其斜率
处的切线,故其斜率 ,
,
所以直线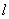 的方程为
的方程为
又因为直线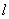 与
与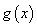 的图象相切,所以
的图象相切,所以 在点
在点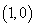 的导函数值为1.
的导函数值为1. 
所以
(2)  ,故
,故 ,
,
若 ,则
,则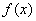 在
在 上递减,在
上递减,在 上递增
上递增
而当 时
时 ,当
,当 时
时
 恰有一解
恰有一解
 即
即
当 时
时
令 得
得 (舍)或
(舍)或 ,符合题意
,符合题意
若 ,则
,则 ,
,
因为 ,则
,则
 ,
,

又 时
时 ,当
,当 时
时
从而 恰有一解;
恰有一解;
若 ,则
,则
 ,
,
当 时
时
所以从而 恰有一解
恰有一解
所以所求 的范围为
的范围为 .
.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
 ,且相互间没有影响.
,且相互间没有影响. 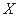 ,试求
,试求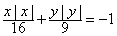 的曲线即为函数
的曲线即为函数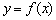 的图像,对于函数
的图像,对于函数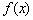 在
在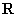 上单调递减;②函数
上单调递减;②函数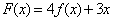 不存在零点;③函数
不存在零点;③函数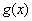 和
和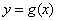 由方程
由方程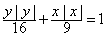 确定.其中所有正确的命题序号是 [答]( )
确定.其中所有正确的命题序号是 [答]( ) ,则
,则 的大小关系为 .
的大小关系为 .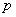 :“函数
:“函数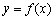 的图像关于点
的图像关于点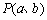 成中心对称图形”的充要条件为“函数
成中心对称图形”的充要条件为“函数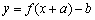 是奇函数”.
是奇函数”.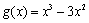 ,求函数
,求函数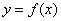 的图像关于某直线成轴对称图像”成立的什么条件?请说明理由.
的图像关于某直线成轴对称图像”成立的什么条件?请说明理由. 的终边过点
的终边过点 ,则
,则 的值为( )
的值为( ) B.
B. C.
C. D.
D.
 ,对
,对 ,使得
,使得 ,则
,则 的最小值为( )
的最小值为( ) B.
B.  C.
C.  D.
D. 
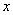 的不等式
的不等式 .(Ⅰ)当
.(Ⅰ)当 时,解此不等式;
时,解此不等式; ,当
,当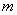 为何值时,
为何值时, 恒成立?
恒成立?