题目内容
数列{an}为各项为正数的等比数列,且a4=2,已知函数f(x)=log
x,则f(a13)+f(a23)+…+f(a73)=( )
| 1 |
| 2 |
| A、-6 | B、-21 |
| C、-12 | D、21 |
考点:数列的求和,对数的运算性质
专题:等差数列与等比数列
分析:利用等差数列的性质可把原式化简可得3×log
(a1•a2…a7),再由等比数列的性质可得a1•a7=a2•a6=a3•a5=a42,从而可得答案.
| 1 |
| 2 |
解答:
解:由等比数列的性质可得,a1•a7=a2•a6=a3•a5=a42,
由于f(a13)+f(a23)+…+f(a73)=log
a13+log
a23+…+log
a73,
=3×(log
a1+log
a2+…+log
a7)=3×log
(a1•a2…a7),
则f(a13)+f(a23)+…+f(a73)=3×log
a47
=21×log
2=-21,
故答案为:B
由于f(a13)+f(a23)+…+f(a73)=log
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=3×(log
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
则f(a13)+f(a23)+…+f(a73)=3×log
| 1 |
| 2 |
=21×log
| 1 |
| 2 |
故答案为:B
点评:本题主要考查了等比数列的性质的综合应用,利用性质可以简化基本运算.若m+n=p+q,则再等差数列中有am+an=ap+aq;在等比数列中有am•an=ap•aq

练习册系列答案
相关题目
三个数a=log53,b=log3
,c=3
大小的顺序是( )
| 2 |
| 1 |
| 5 |
| A、a>b>c |
| B、a>c>b |
| C、c>b>a |
| D、c>a>b |
两圆x2+y2-4x+6y=0和x2+y2-6x=0的连心线方程为( )
| A、x+y+3=0 |
| B、2x-y-5=0 |
| C、3x-y-9=0 |
| D、4x-3y+7=0 |
 已知
已知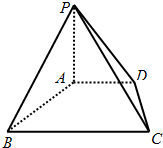 已知四棱锥P-ABCD的底面ABCD是直角梯形,AD∥BC,∠ABC=90°,PA⊥平面ABCD,AB=BC=2AD,若平面PCD与平面PAB所成二面角的余弦值为
已知四棱锥P-ABCD的底面ABCD是直角梯形,AD∥BC,∠ABC=90°,PA⊥平面ABCD,AB=BC=2AD,若平面PCD与平面PAB所成二面角的余弦值为