题目内容
已知函数f(x)定义域为[0,+∞),且对任意非负实数x,y都有f(x+y)=f(x)+f(y)-3,且x>0时f(x)<3.
(1)求f(0);
(2)判断f(x)在定义域上的单调性,并给出证明;
(3)若f(1)=1且f(x2-x)+f(8-5x)≥0,求x的取值范围.
(1)求f(0);
(2)判断f(x)在定义域上的单调性,并给出证明;
(3)若f(1)=1且f(x2-x)+f(8-5x)≥0,求x的取值范围.
考点:抽象函数及其应用,函数单调性的判断与证明,函数单调性的性质
专题:函数的性质及应用
分析:(1)利用赋值法,x=y=0直接求解f(0)即可;
(2)根据定义进行直接判定,设x1>x2≥0,则f(x1)-f(x2)=f[x2+(x1-x2)]-f(x2)=f(x2)+f(x1-x2)-f(x2)-3=f(x1-x2)-3然后判断符号,即可得到函数的单调性;
(3)先根据已知条件得到f(3)=-3,再根据函数的单调性将所求不等式转化为0≤x2-6x+8≤3,从而可求出x的取值范围.
(2)根据定义进行直接判定,设x1>x2≥0,则f(x1)-f(x2)=f[x2+(x1-x2)]-f(x2)=f(x2)+f(x1-x2)-f(x2)-3=f(x1-x2)-3然后判断符号,即可得到函数的单调性;
(3)先根据已知条件得到f(3)=-3,再根据函数的单调性将所求不等式转化为0≤x2-6x+8≤3,从而可求出x的取值范围.
解答:
解:(1)∵对任意非负实数x,y都有f(x+y)=f(x)+f(y)-3,
∴令x=0,y=0,得f(0)=2f(0)-3,
∴f(0)=3;
(2)设x1>x2≥0,则f(x1)-f(x2)=f[x2+(x1-x2)]-f(x2)=f(x2)+f(x1-x2)-f(x2)-3=f(x1-x2)-3,
∵x1-x2>0 且当x>0时f(x)<3,则f(x1-x2)<3
∴f(x1)-f(x2)<0,
∴f(x)在定义域上单调递减,
(3)由f(x)定义域得x2-x≥0,8-5x≥0,解得 x∈(-∞,0]∪[1,
]…①
∵对任意非负实数x,y都有f(x+y)=f(x)+f(y)-3,
∴f(x2-x)+f(8-5x)=f(x2-6x+8)+3≥0,
即f(x2-6x+8)≥-3,
∵f(1)=1 则f(2)=1+1-3=-1,f(3)=f(1)+f(2)-3=-3
不等式可以化为f(x2-6x+8)≥f(3),
∵f(x)在定义域上单调递减,
∴0≤x2-6x+8≤3,
解得x∈[1,2]∪[4,5]…②
综合①②可得,x取值范围是[1,
].
∴令x=0,y=0,得f(0)=2f(0)-3,
∴f(0)=3;
(2)设x1>x2≥0,则f(x1)-f(x2)=f[x2+(x1-x2)]-f(x2)=f(x2)+f(x1-x2)-f(x2)-3=f(x1-x2)-3,
∵x1-x2>0 且当x>0时f(x)<3,则f(x1-x2)<3
∴f(x1)-f(x2)<0,
∴f(x)在定义域上单调递减,
(3)由f(x)定义域得x2-x≥0,8-5x≥0,解得 x∈(-∞,0]∪[1,
| 8 |
| 5 |
∵对任意非负实数x,y都有f(x+y)=f(x)+f(y)-3,
∴f(x2-x)+f(8-5x)=f(x2-6x+8)+3≥0,
即f(x2-6x+8)≥-3,
∵f(1)=1 则f(2)=1+1-3=-1,f(3)=f(1)+f(2)-3=-3
不等式可以化为f(x2-6x+8)≥f(3),
∵f(x)在定义域上单调递减,
∴0≤x2-6x+8≤3,
解得x∈[1,2]∪[4,5]…②
综合①②可得,x取值范围是[1,
| 8 |
| 5 |
点评:此题是个难题,考查抽象函数及其应用,以及利用函数单调性的定义判断函数的单调性,并根据函数的单调性解函数值不等式,体现了转化的思想,在转化过程中一定注意函数的定义域,解决抽象函数的问题一般应用赋值法.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
已知x,y∈R,则( )
| A、lg(2x+2y)=lg2x+lg2y |
| B、lg(2x•2y)=lg2x•lg2y |
| C、lg(2x+y)=lg2x•lg2y |
| D、lg(2x+y)=lg2x+lg2y |
数列{an}为各项为正数的等比数列,且a4=2,已知函数f(x)=log
x,则f(a13)+f(a23)+…+f(a73)=( )
| 1 |
| 2 |
| A、-6 | B、-21 |
| C、-12 | D、21 |
“1,x,9成等比数列”是“x=3”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
已知集合A={x|x2-
x-k=0,x∈(-1,1)},若集合A有且仅有一个元素,则实数k的取值范围是( )
| 3 |
| 2 |
A、(-
| ||||||
B、(
| ||||||
C、[-
| ||||||
D、[-
|

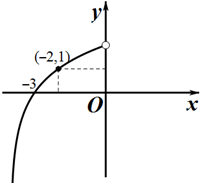 已知函数f(x)是定义域为R的奇函数.当x<0时,f(x)=loga(x+b),图象如图所示.
已知函数f(x)是定义域为R的奇函数.当x<0时,f(x)=loga(x+b),图象如图所示.