题目内容
偶函数y=f(x)的图象关于直线x=2对称,f(3)=3,则f(-1)= .
考点:函数奇偶性的性质
专题:函数的性质及应用
分析:根据函数奇偶性和对称性的性质,得到f(x+4)=f(x),即可得到结论.
解答:
解:因为偶函数y=f(x)的图象关于直线x=2对称,
所以f(2+x)=f(2-x)=f(x-2),
即f(x+4)=f(x),
则f(-1)=f(-1+4)=f(3)=3,
故答案为:3.
所以f(2+x)=f(2-x)=f(x-2),
即f(x+4)=f(x),
则f(-1)=f(-1+4)=f(3)=3,
故答案为:3.
点评:本题主要考查函数值的计算,利用函数奇偶性和对称性的性质得到周期性f(x+4)=f(x)是解决本题的关键,比较基础.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
定积分
(2x+ex)dx的值为( )
| ∫ | 1 0 |
| A、e+2 | B、e+1 |
| C、e | D、e-1 |

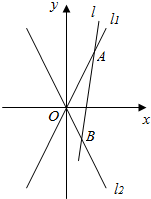 已知双曲线E:
已知双曲线E: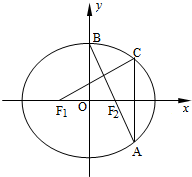 如图,在平面直角坐标系xOy中,F1,F2分别为椭圆
如图,在平面直角坐标系xOy中,F1,F2分别为椭圆 如图,在边长为1的正方形中随机撒1000粒豆子,有180粒落到阴影部分,据此估计阴影部分的面积为
如图,在边长为1的正方形中随机撒1000粒豆子,有180粒落到阴影部分,据此估计阴影部分的面积为