题目内容
从集合{1,2,3,4,5,6,7,8,9,10}中任取两个数,欲使取到的一个数大于k,另一个数小于k(其中k∈{5,6,7,8,9})的概率是
,则k= .
| 2 |
| 5 |
考点:古典概型及其概率计算公式
专题:概率与统计
分析:,先求出所有的基本事件有45种,再求出取到的一个数大于k,另一个数小于k的基本事件有(k-1)(10-k),根据古典概率公式即可得到关于k的方程解得即可
解答:
解:从集合{1,2,3,4,5,6,7,8,9,10}中任取两个数的基本事件有
=45种,
取到的一个数大于k,另一个数小于k,比k的小的数有(k-1)个.比k的大的数有(10-k)个,故有
•
=(k-1)(10-k),
所以取到的一个数大于k,另一个数小于k(其中k∈{5,6,7,8,9})的概率是P=
=
,
解得k=7
故答案为:7
| C | 2 10 |
取到的一个数大于k,另一个数小于k,比k的小的数有(k-1)个.比k的大的数有(10-k)个,故有
| C | 1 k-1 |
| C | 1 10-k |
所以取到的一个数大于k,另一个数小于k(其中k∈{5,6,7,8,9})的概率是P=
| (k-1)(10-k) |
| 45 |
| 2 |
| 5 |
解得k=7
故答案为:7
点评:本题考查了古典概型的概率公式的应用,关键是求出取到的一个数大于k,另一个数小于k的基本事件,属于基础题

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已f(x)=2sin(
x+
),f(x)的最小正周期是( )
| π |
| 2 |
| π |
| 3 |
| A、2 | B、4π | C、2π | D、4 |
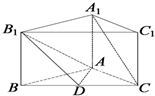 如图,正三棱柱(底面是正三角形且侧棱垂直底面的三棱柱)ABC-A1B1C1中,
如图,正三棱柱(底面是正三角形且侧棱垂直底面的三棱柱)ABC-A1B1C1中, 如图,四棱锥P-ABCD的底面是一直角梯形,AB∥CD,BA⊥AD,CD=2AB,PA⊥底面ABCD,E为PC的中点,则BE与平面PAD的位置关系为
如图,四棱锥P-ABCD的底面是一直角梯形,AB∥CD,BA⊥AD,CD=2AB,PA⊥底面ABCD,E为PC的中点,则BE与平面PAD的位置关系为