题目内容
14.在等差数列{an}中,a5a7=6,a2+a10=5,则a10-a6=±2.分析 由已知列式求得a5、a7的值,进一步求出公差,则由a10-a6=4d得答案.
解答 解:在等差数列{an}中,由a2+a10=5,得a5+a7=5,
又a5a7=6,
∴$\left\{\begin{array}{l}{{a}_{5}=2}\\{{a}_{7}=3}\end{array}\right.$或$\left\{\begin{array}{l}{{a}_{5}=3}\\{{a}_{7}=2}\end{array}\right.$,
若$\left\{\begin{array}{l}{{a}_{5}=2}\\{{a}_{7}=3}\end{array}\right.$,则d=$\frac{1}{2}$;
若$\left\{\begin{array}{l}{{a}_{5}=3}\\{{a}_{7}=2}\end{array}\right.$,则d=$-\frac{1}{2}$.
∴a10-a6=4d=±2.
故答案为:±2.
点评 本题考查等差数列的通项公式,考查等差数列的性质,是基础的计算题.

练习册系列答案
 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
4.已知命题$p:t=\frac{π}{2}$,命题q:${∫}_{0}^{t}$sinxdx=1,则p是q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
5.为检测空气质量,某市环保局随机抽取了甲、乙两地2016年20天PM2.5日平均浓度(单位:微克/立方米)监测数据,得到甲地PM2.5日平均浓度频率分布直方图和乙地PM2.5日平均浓度的频数分布表.

乙地20天PM2.5日平均浓度频数分布表
(1)根据乙地20天PM2.5日平均浓度的频率分布表作出相应的频率分组直方图,并通过两个频率分布直方图比较两地PM2.5日平均浓度的平均值及分散程度(不要求计算出具体值,给出结论即可);
(2)通过调查,该市市民对空气质量的满意度从高到低分为三个等级:
记事件C:“甲地市民对空气质量的满意度等级高于乙地市民对空气质量的满意度等级”,假设两地市民对空气质量满意度的调查结果相互独立,根据所给数据,利用样本估计总体的统计思想,以事件发生的频率作为相应事件发生的概率,求事件C的概率.

乙地20天PM2.5日平均浓度频数分布表
| PM2.5日平均浓度(微克/立方米) | [0,20] | (20,40] | (40,60] | (60,80] | (80,100] |
| 频数(天) | 2 | 3 | 4 | 6 | 5 |
(2)通过调查,该市市民对空气质量的满意度从高到低分为三个等级:
| 满意度等级 | 非常满意 | 满意 | 不满意 |
| PM2.5日平均浓度(微克/立方米) | 不超过20 | 大于20不超过60 | 超过60 |
9.一个三棱锥的三视图如图(图中小正方形的边长为1),则这个三棱锥的体积是( )
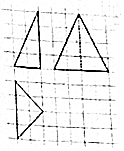

| A. | $\frac{32}{3}$ | B. | 8 | C. | $\frac{20}{3}$ | D. | $\frac{16}{3}$ |
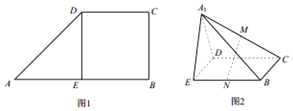 如图1.在直角梯形ABCD中,AB∥CD,AB⊥BC,AB=2CD,DE⊥AB,沿DE将△AEDD折起到△A1ED的位置,连结A1B,A1C,M,N分别为A1C,BE的中点.如图2.
如图1.在直角梯形ABCD中,AB∥CD,AB⊥BC,AB=2CD,DE⊥AB,沿DE将△AEDD折起到△A1ED的位置,连结A1B,A1C,M,N分别为A1C,BE的中点.如图2.