题目内容
已知△ABC外接圆的半径为1，圆心为O，且2
+
+
=0，|
|=|
|，E，F为边AC的三等分点，则
•
= ．
| OA |
| AB |
| AC |
| OA |
| AB |
| BE |
| BF |
考点：平面向量数量积的运算
专题：平面向量及应用
分析：如图所示，设D为BC的中点，则
+
=2
，由于2
+
+
=0，可得2
+2
=
，即D与O点重合．由于|
|=|
|，可得△OAB是等边三角形，AB=1，AC=
．由于E，F为边AC的三等分点，可得E(0，
)，F(0，
)．再利用数量积运算即可得出．
| AB |
| AC |
| AD |
| OA |
| AB |
| AC |
| OA |
| AD |
| 0 |
| OA |
| AB |
| 3 |
| ||
| 3 |
2
| ||
| 3 |
解答：
解：如图所示，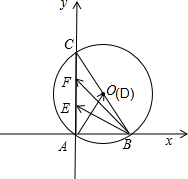
设D为BC的中点，则
+
=2
，
∵2
+
+
=0，∴2
+2
=
，∴
=
，即D与O点重合．
∵|
|=|
|，∴△OAB是等边三角形．
∴AB=1，AC=
．
∵E，F为边AC的三等分点，∴E(0，
)，F(0，
)．
又B（1，0），
∴
•
=(-1，
)•(-1，
)=1+
=
．
故答案为：
．
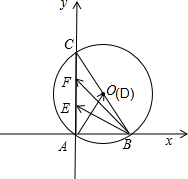
设D为BC的中点，则
| AB |
| AC |
| AD |
∵2
| OA |
| AB |
| AC |
| OA |
| AD |
| 0 |
| OD |
| 0 |
∵|
| OA |
| AB |
∴AB=1，AC=
| 3 |
∵E，F为边AC的三等分点，∴E(0，
| ||
| 3 |
2
| ||
| 3 |
又B（1，0），
∴
| BE |
| BF |
| ||
| 3 |
2
| ||
| 3 |
| 2 |
| 3 |
| 5 |
| 3 |
故答案为：
| 5 |
| 3 |
点评：本题考查了向量的平行四边形法则、坐标运算、数量积运算、等边三角形的性质，考查了推理能力和计算能力，属于中档题．
练习册系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
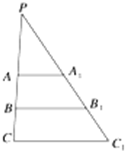棱台的上底面积为16，下底面积为64，求棱台被它的中截面分成的上、下两部分体积之比．
如图，在Rt△AOB中，∠AOB=90°，OA=2，OB=3，若