题目内容
20.设锐角三角形ABC的内角A,B,C的对边分别为a,b,c,且a=2bsin A.(Ⅰ)求角B的大小;
(Ⅱ)若a=$3\sqrt{3}$,c=5,求△ABC的面积及b.
分析 (Ⅰ)由已知及正弦定理得sin A=2sin Bsin A,由于sin A≠0,可求sinB=$\frac{1}{2}$,结合B是锐角,可求B.
(Ⅱ)依题意利用三角形面积公式及余弦定理即可计算得解.
解答 (本题满分为12分)
解:(Ⅰ)因为a=2bsin A,由正弦定理得sin A=2sin Bsin A,…(2分)
由于sin A≠0,故有sin B=$\frac{1}{2}$,…(4分)
又因为B是锐角,所以B=30°.…(5分)
(Ⅱ)依题意得:S△ABC=$\frac{1}{2}$acsin 30°=$\frac{1}{2}$×3$\sqrt{3}$×5×$\frac{1}{2}$=$\frac{15\sqrt{3}}{4}$,…(8分)
所以由余弦定理b2=a2+c2-2accos B,可得:
b2=(3$\sqrt{3}$)2+52-2×3$\sqrt{3}$×5×cos 30°=27+25-45=7,…(11分)
所以b=$\sqrt{7}$.…(12分)
点评 本题主要考查了正弦定理,三角形面积公式及余弦定理在解三角形中的应用,考查了计算能力和转化思想,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.已知向量$\overrightarrow{AB}=(2,-1)$,$\overrightarrow{AC}=(-4,1)$,向量$\overrightarrow{BC}$的坐标是( )
| A. | (-6,2) | B. | (6,-2) | C. | (-2,0) | D. | (2,0) |
8.已知命题p1:?x0∈R,x02+x0+1<0;p2:?x∈[1,2],x2-1≥0.以下命题为真命题的是( )
| A. | (¬p1)∧(¬p2) | B. | p1∨(¬p2) | C. | (¬p1)∧p2 | D. | p1∧p2 |
12.已知sinα=$\frac{3}{5}$$(\frac{π}{2}<α<π)$,则$sin(α-\frac{π}{3})$=( )
| A. | $\frac{{4\sqrt{3}-3}}{10}$ | B. | $\frac{{4\sqrt{3}+3}}{10}$ | C. | $\frac{{3-4\sqrt{3}}}{10}$ | D. | $\frac{{4\sqrt{3}+3}}{5}$ |
9.根据如图的流程图,可得的结果是( )
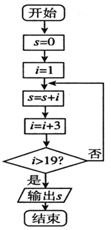

| A. | 76 | B. | 70 | C. | 51 | D. | 19 |