题目内容
已知数列{an}的前n项和为Sn,点(an,Sn)在直线y=3x+4上.
(1)求数列{an}的通项an;
(2)令bn=nan(n∈N+),试求数列{bn}的前n项和Tn.
(1)求数列{an}的通项an;
(2)令bn=nan(n∈N+),试求数列{bn}的前n项和Tn.
考点:数列的求和
专题:计算题,等差数列与等比数列
分析:(1)由点(an,Sn)在直线y=3x+4上,得Sn=3an+4,又Sn+1=3an+1+4,两式相减可得数列递推式,根据递推式可判断该数列为等比数列,从而可求an;
(2)由(1)表示出bn,利用错位相减法可求得Tn.
(2)由(1)表示出bn,利用错位相减法可求得Tn.
解答:
解:(1)∵点(an,Sn)在直线y=3x+4上,
∴Sn=3an+4,Sn+1=3an+1+4,
两式相减,得an+1=Sn+1-Sn=3an+1-3an,化简得2an+1=3an,
数列{an}为等比数列,公比q=
,
由S1=a1=3a1+4,得a1=-2,
故an=a1qn-1=-2(
)n-1(n∈N*).
(2)∵bn=nan=-2n(
)n-1(n∈N+),
∴Tn=b1+b2+b3+b4+…+bn-1+bn
=-2[1+2×
+3×(
)2+4×(
)3+…+(n-1)×(
)n-2+n×(
)n-1],①
×Tn=-2[
+2×(
)2+3×(
)3+4×(
)4+…+(n-1)×(
)n-1+n×(
)n],②
①-②得-
Tn=-2[1+
+(
)2+(
)3+…+(
)n-1-n×(
)n],
Tn=4[1+
+(
)2+(
)3+…+(
)n-1-n×(
)n]
=4×
-4n×(
)n=4(2-n)•(
)n-8(n∈N*).
∴Sn=3an+4,Sn+1=3an+1+4,
两式相减,得an+1=Sn+1-Sn=3an+1-3an,化简得2an+1=3an,
数列{an}为等比数列,公比q=
| 3 |
| 2 |
由S1=a1=3a1+4,得a1=-2,
故an=a1qn-1=-2(
| 3 |
| 2 |
(2)∵bn=nan=-2n(
| 3 |
| 2 |
∴Tn=b1+b2+b3+b4+…+bn-1+bn
=-2[1+2×
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
①-②得-
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
Tn=4[1+
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
=4×
1-(
| ||
1-
|
| 3 |
| 2 |
| 3 |
| 2 |
点评:本题考查由递推式求数列通项、等比数列的概念及数列求和,错位相减法对数列求和是高考考查的重点内容,要熟练掌握.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
若连续抛掷两次骰子得到的点数分别为m,n,m+n=5的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
已知复数z=
,其中i是虚数单位,则z的虚部为( )
| 2i |
| 1+i |
| A、2 | B、-2 | C、1 | D、-1 |
二项式(x2-
)n的展开式中各项系数的和为( )
| 1 |
| x |
| A、32 | B、-32 | C、0 | D、1 |
当0<x<
时,函数f(x)=
的最小值为( )
| π |
| 2 |
| 3sin2x+1 |
| tanxcos2x |
| A、2 | ||
B、2
| ||
| C、4 | ||
D、4
|
 为了了解调研高一年级新学生的智力水平,某校按l 0%的比例对700名高一学生按性别分别进行“智力评分”抽样检查,测得“智力评分”的频数分布表如表l,表2.
为了了解调研高一年级新学生的智力水平,某校按l 0%的比例对700名高一学生按性别分别进行“智力评分”抽样检查,测得“智力评分”的频数分布表如表l,表2.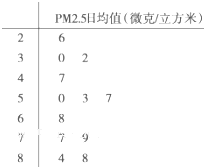 PM2.5是指悬浮在空气中的空气动力学当量直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物,根据现行国家标准GB3095-2012,PM2.5日均值在35微克/立方米以下空气质量为一级;在35微克/立方米~75毫克/立方米之间空气质量为二级;在75微克/立方米以上空气质量为超标.从某自然保护区2012年全年每天的PM2.5监测值数据中随机地抽取12天的数据作为样本,监测值如茎叶图所示(十位为茎,个位为叶):
PM2.5是指悬浮在空气中的空气动力学当量直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物,根据现行国家标准GB3095-2012,PM2.5日均值在35微克/立方米以下空气质量为一级;在35微克/立方米~75毫克/立方米之间空气质量为二级;在75微克/立方米以上空气质量为超标.从某自然保护区2012年全年每天的PM2.5监测值数据中随机地抽取12天的数据作为样本,监测值如茎叶图所示(十位为茎,个位为叶):