题目内容
若不等式|x+2|+|x-3|≥a+
对任意的实数x恒成立,则实数a的取值范围是 .
| 4 |
| a-1 |
考点:绝对值不等式的解法
专题:计算题,不等式的解法及应用
分析:不等式|x+2|+|x-3|≥a+
对任意的实数x恒成立,转化为a+
小于等于函数y=|x+2|+|x-3|的最小值,根据绝对值不等式的几何意义可知函数y=|x+2|+|x-3|的最小值为5,因此原不等式转化为分式不等式的求解问题.
| 4 |
| a-1 |
| 4 |
| a-1 |
解答:
解:令y=|x+2|+|x-3|,
由绝对值不等式的几何意义可知
函数y=|x+2|+|x-3|的最小值为5,
∵不等式|x+2|+|x-3|≥a+
对任意的实数x恒成立,
∴原不等式可化为a+
≤5,
解得a=3或a<1,
故答案为:(-∞,1)∪{3}.
由绝对值不等式的几何意义可知
函数y=|x+2|+|x-3|的最小值为5,
∵不等式|x+2|+|x-3|≥a+
| 4 |
| a-1 |
∴原不等式可化为a+
| 4 |
| a-1 |
解得a=3或a<1,
故答案为:(-∞,1)∪{3}.
点评:考查绝对值不等式的几何意义,把恒成立问题转化为求函数的最值问题,体现了转化的思想方法,属中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知集合A={x|-1≤x≤1},B={x|x2-2x≤0},则A∩(∁RB)=( )
| A、[-1,0) |
| B、[-1,0] |
| C、[0,1] |
| D、(-∞,1]∪[2,+∞) |
已知变量x、y满足的约束条件
,则z=3x+2y的最大值为( )
|
| A、-3 | ||
B、
| ||
| C、4 | ||
| D、-5 |
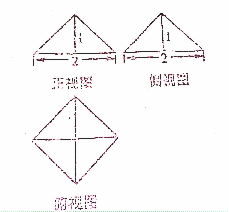 某几何体的三视图如图所示,其中正视图、侧视图均为斜边等于2的等腰直角三角形,俯视图是对角线为2的正方形,则该几何体的内切球的半径等于
某几何体的三视图如图所示,其中正视图、侧视图均为斜边等于2的等腰直角三角形,俯视图是对角线为2的正方形,则该几何体的内切球的半径等于 如图是抛物线型拱桥,在平时,水面离拱顶3米,水面宽为2
如图是抛物线型拱桥,在平时,水面离拱顶3米,水面宽为2