题目内容
9.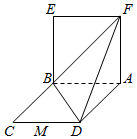 已知四边形ABCD为平行四边形,BD⊥AD,BD=AD,AB=2,四边形ABEF为正方形,且平面ABEF⊥平面ABCD.
已知四边形ABCD为平行四边形,BD⊥AD,BD=AD,AB=2,四边形ABEF为正方形,且平面ABEF⊥平面ABCD.(1)求证:BD⊥平面ADF;
(2)若M为CD中点,证明:在线段EF上存在点N,使得MN∥平面ADF,并求出此时三棱锥N-ADF的体积.
分析 (1)证明AF⊥平面ABCD,得出AF⊥BD,再由BD⊥AD即可得出BD⊥平面ADF;
(2)N为线段EF中点时,MN∥平面ADF,证明时利用正方形ABEF与平行四边形形ABCD的性质,得出四边形NFDM为平行四边形,从而证得MN∥DF,MN∥平面ADF,利用等积法求出三棱锥N-ADF的条件即可.
解答 解:(1)证明:正方形ABEF中,AF⊥AB,
∵平面ABEF⊥平面ABCD,又AF?平面ABEF,
平面ABEF∩平面ABCD=AB,
∴AF⊥平面ABCD;
又∵BD?平面ABCD,
∴AF⊥BD;
又BD⊥AD,AF∩AD=A,AF、AD?平面ADF,
∴BD⊥平面ADF;
(2)当N为线段EF中点时,MN∥平面ADF;
证明如下:正方形ABEF中,NF$\stackrel{∥}{=}$$\frac{1}{2}$BA,
平行四边形形ABCD中,MD$\stackrel{∥}{=}$$\frac{1}{2}$BA,
∴NF$\stackrel{∥}{=}$MD,
∴四边形NFDM为平行四边形,
∴MN∥DF;
又DF?平面ADF,MN?平面ADF,
∴MN∥平面ADF,过D作DH⊥AB于H,
∵平面ABEF⊥平面ABCD,
又DH?平面ABCD,平面ABEF∩平面ABCD=AB,
∴DH⊥平面ABEF;
在Rt△ABD中,AB=2,BD=AD,
∴DH=1,
∴V三棱锥N-ADF=V三棱锥D-ANF
=$\frac{1}{3}$DH•S△ANF
=$\frac{1}{3}$×1×$\frac{1}{2}$×1×2
=$\frac{1}{3}$.
点评 本题考查了空间中的平行与垂直关系的应用问题,也考查了利用等积法求三棱锥体积的应用问题,是综合性题目.

练习册系列答案
相关题目
9.下列变量中,不是随机变量的是( )
| A. | 掷一枚骰子,所得的点数 | B. | 一射手射击一次,击中的环数 | ||
| C. | 某日上证收盘指数 | D. | 标准状态下,水在100℃时会沸腾 |
18.双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$为等轴曲线,过右焦点F作x轴的垂线交双曲线与A,B两点,若|AB|=2$\sqrt{2}$,△OAB(O为坐标原点)的面积为( )
| A. | 2$\sqrt{2}$ | B. | 2$\sqrt{3}$ | C. | 4$\sqrt{2}$ | D. | 4$\sqrt{3}$ |