题目内容
已知
=(1,1),
=(1,t),若
与
夹角为锐角,则t的取值范围是 .
| a |
| b |
| a |
| b |
考点:平面向量数量积的坐标表示、模、夹角
专题:平面向量及应用
分析:设
与
夹角为锐角θ,则cosθ=
>0,且cosθ≠1.解出即可.
| a |
| b |
| ||||
|
|
解答:
解:设
与
夹角为锐角θ,∵
=(1,1),
=(1,t),
∴
•
=1+t,|
|=
,|
|=
.
∴cosθ=
=
>0,且cosθ≠1.
解得t>-1,且t≠1.
∴t的取值范围是(-1,1)∪(1,+∞).
故答案为:是(-1,1)∪(1,+∞).
| a |
| b |
| a |
| b |
∴
| a |
| b |
| a |
| 2 |
| b |
| 1+t2 |
∴cosθ=
| ||||
|
|
| 1+t | ||||
|
解得t>-1,且t≠1.
∴t的取值范围是(-1,1)∪(1,+∞).
故答案为:是(-1,1)∪(1,+∞).
点评:本题考查了向量的夹角公式、数量积运算,属于中档题.

练习册系列答案
相关题目
若数列{an}满足
-
=d(n∈N*,d为常数),则称数列{an}为“调和数列”,已知正项数列{
}为“调和数列”,且b1+b2+…+b11=110,则b5•b7的最大值是( )
| 1 |
| an+1 |
| 1 |
| an |
| 1 |
| bn |
| A、10 | B、100 |
| C、110 | D、200 |
在△ABC中,已知a=
,b=1,A=45°,则B等于( )
| 2 |
| A、30° |
| B、60° |
| C、30°或150° |
| D、60°或120° |
已知等比数列{an}满足an>0,n=1,2,…,a5•a2n-5=22n,(n≥3),则当n≥1时,log2a1+log2a3+…+log2a2n+1=( )
| A、n(2n-1) |
| B、n2 |
| C、(n+1)2 |
| D、(n-1)2 |
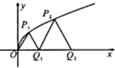 如图,抛物线y=
如图,抛物线y=