题目内容
19.小王同学骑电动自行车以24km/h的速度沿着正北方向的公路行驶,在点A处望见电视塔S在电动车的北偏东30°方向上,20min后到点B处望见电视塔在电动车的北偏东75°方向上,则电动车在点B时与电视塔S的距离是$4\sqrt{2}$km.分析 在△ABS中,可得∠BAS=30°,AB=8,∠ABS=180°-75°=105°则∠ASB=45°,由正弦定理可得BS=$\frac{ABsin30°}{sin45°}$.
解答 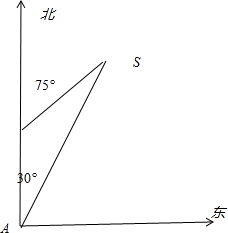 解:如图,由已知可得,AB=24×$\frac{20}{60}$=8.
解:如图,由已知可得,AB=24×$\frac{20}{60}$=8.
在△ABS中,∠BAS=30°,AB=8,∠ABS=180°-75°=105°
∠ASB=45°
由正弦定理可得BS=$\frac{ABsin30°}{sin45°}$=4$\sqrt{2}$,
故答案为$4\sqrt{2}$
点评 本题主要考查了正弦定理在实际问题中的应用,解题的关键是要把实际问题转化为数学问题.进而利用数学基本知识进行求解.

练习册系列答案
相关题目
9.已知圆C:x2+y2+2x-4y=0,则圆C的圆心坐标为( )
| A. | (1,-2) | B. | (-1,2) | C. | (1,2) | D. | (-1,-2) |
7.已知$f(x)=\left\{\begin{array}{l}(4-a)x\;,\;\;x∈(-∞\;,\;1]\\{a^x}\;,\;\;\;x∈(1\;,\;+∞)\end{array}\right.$是R上的增函数,那么实数a的取值范围是( )
| A. | (1,4) | B. | [1,4) | C. | (2,4) | D. | [2,4) |
4.二次函数f(x)=ax2+bx+1的最小值为f(1)=0,则a-b=( )
| A. | -2 | B. | -1 | C. | 1 | D. | 3 |
11.已知向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角是120°,且|$\overrightarrow{a}$|=5,|$\overrightarrow{b}$|=4,则$\overrightarrow{a}$•$\overrightarrow{b}$=( )
| A. | 20 | B. | 10 | C. | -10 | D. | -20 |
9.“0<a<1”是“a<$\sqrt{a}$”的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |