题目内容
曲线C:
(α为参数),若以点O(0,0)为极点,x轴正半轴为极轴建立极坐标系,则该曲线的极坐标方程是 .
|
考点:参数方程化成普通方程
专题:坐标系和参数方程
分析:曲线C:
,消去参数α可得(x+2)2+y2=4.把
代入化简即可得出.
|
|
解答:
解:曲线C:
,消去参数α可得(x+2)2+y2=4.
把
代入可得(ρcosθ+2)2+(ρsinθ)2=4.
化为ρ=-4cosθ.
故答案为:ρ=-4cosθ.
|
把
|
化为ρ=-4cosθ.
故答案为:ρ=-4cosθ.
点评:本题考查了参数方程化为普通方程、直角坐标方程化为极坐标方程,考查了计算能力,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

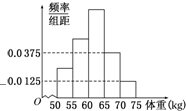 如图是某学校抽取的学生体重的频率分布直方图,已知图中从左到右的前3个小组的频率之比为1:2:3,第2小组的频数为10,则抽取的学生人数为( )
如图是某学校抽取的学生体重的频率分布直方图,已知图中从左到右的前3个小组的频率之比为1:2:3,第2小组的频数为10,则抽取的学生人数为( )