题目内容
 已知an=(
已知an=(| 1 |
| 2 |
(1)A(4,5)=
(2)A(m,n)=
考点:归纳推理
专题:综合题,推理和证明
分析:通过观察给出图形的特点,得到图形中的每一行所占数列{an}的项的个数构成以1为首项,以2为公差的等差数列,然后运用等差数列前n项和公式,则问题得到解决.
解答:
解:由三角形状图可知,图中的第一行、第二行、第三行、…分别占了数列{an}的1项、3项、5项、…,
每一行的项数构成了以1为首项,以2为公差的等差数列,
设A(m,n)是数列{an}的第k项,则
(1)A(4,5)是数列{an}的第1+3+5+5=14项,所以A(4,5)=(
)14,
(2)A(m,n)是数列{an}的第1+3+5+…+(2m-3)+n=(m-1)2+n项,故A(m,n)=(
)(m-1)2+n.
故答案为:(
)14,(
)(m-1)2+n
每一行的项数构成了以1为首项,以2为公差的等差数列,
设A(m,n)是数列{an}的第k项,则
(1)A(4,5)是数列{an}的第1+3+5+5=14项,所以A(4,5)=(
| 1 |
| 2 |
(2)A(m,n)是数列{an}的第1+3+5+…+(2m-3)+n=(m-1)2+n项,故A(m,n)=(
| 1 |
| 2 |
故答案为:(
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了等差数列的定义及通项公式,考查了学生的读图能力,考查了数学转化思想方法,解答此题的关键是求解A(m,n)是数列{an}的第1+3+5+…+(2m-3)+n=(m-1)2+n项,此题是中档题.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
已知
,
为不共共线的非零向量,且|
|=|
|=1,则以下四个向量中模最大者为( )
| e1 |
| e2 |
| e1 |
| e2 |
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
已知关于x的方程:
x2+
2x+
=
(x∈R),其中点C为直线AB上一点,O是直线外一点,则下列结论正确的是( )
| OA |
| OB |
| OC |
| O |
| A、点C在线段AB上 |
| B、点C在线段AB的延长线上且点B为线段AC的中点 |
| C、点C在线段AB的反向延长线上且点A为线段BC的中点 |
| D、以上均为可能 |
已知点A(x,1,2)和点B(2,3,4),且|AB|=2
,则实数x的值是( )
| 6 |
| A、-3或4 | B、3或-4 |
| C、6或-2 | D、6或2 |
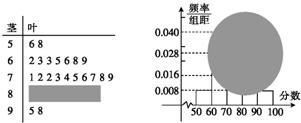 某校高三(1)班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏,但可见部分如图,据此解答如下问题:
某校高三(1)班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏,但可见部分如图,据此解答如下问题: