题目内容

15．“a＜-3”是“f（x）=ax+3在区间（-1，2）上存在零点x0”的（　　）
A．充分不必要条件B．必要不充分条件
C．充要条件D．既不充分也不必要条件

分析 根据充分条件和必要条件的定义结合函数零点的性质进行判断即可．

解答 解：∵f（x）=ax+3在区间（-1，2）上存在零点x0，
∴f（-1）f（2）＜0，即（-a+3）（2a+3）＜0，
则（a-3）（2a+3）＞0，得a＞3或a＜$-\frac{3}{2}$，
则“a＜-3”是“f（x）=ax+3在区间（-1，2）上存在零点x0”的充分不必要条件，
故选：A．

点评 本题主要考查充分条件和必要条件的判断，利用函数零点的存在条件求出a的取值范围是解决本题的关键．

练习册系列答案
相关题目
5．已知函数f（x）=$\frac{\sqrt{3}}{2}$sin2x-cos2x-$\frac{1}{2}$（x∈R），设△ABC的内角A，B，C对应边分别为a，b，c，且c=$\sqrt{3}$，f（C）=0．
（1）求C的值．
（2）若向量$\overrightarrow{m}$=（1，sinA）与向量$\overrightarrow{n}$=（2，sinB）共线，求△ABC的面积．
6．已知集合M={x|$\frac{x-3}{x+1}$＜0}，N={x|x≤-1}，则集合{x|x≥3}等于（　　）
A．M∩NB．M∪NC．∁R（M∩N）D．∁R（M∪N）
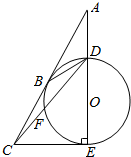3．如图，由圆O外一点A引圆的切线AB和割线ADE，B为切点，DE为圆O的直径，且AD=DB．延长AB至C使得CE与圆O相切，连结CD交圆O于点F．
（Ⅰ）求$\frac{DE}{CE}$．
（Ⅱ）若圆O的半径为1，求CF．
10．已知p：x∈A={x|x2+ax+b≤0，a∈R，b∈R}，q：x∈B={x|x2-2mx+m2-4＜0，m∈R}．
（1）若A={x|-1≤x≤4}，求a+b的值；
（2）在（1）的条件下，若￢q是p的必要条件，求实数m的取值范围．
20．过点M（5，-2），且在x轴、y轴上截距互为相反数的直线方程为（　　）
A．x+y-3=0B．x+y-3=0或2x+5y=0
C．x-y-7=0或2x+5y=0D．x-y-7=0或x+y-3=0
7．椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的上顶点为A，P（$\frac{4\sqrt{2}}{3}$，$\frac{b}{3}$）是C上的一点，以AP为直径的圆经过椭圆C的右焦点F．
（1）求椭圆C的方程；
（2）若直线l：y=kx+m（|k|≤$\frac{\sqrt{2}}{2}$）与椭圆C相交于A、B两点，M为椭圆C上任意一点，且线段OM的中点与线段AB的中点重合，求|OM|的取值范围．
4．求函数f（x）=$\sqrt{2sinx+1}$+lg（5-x）-lg（5+x）的定义域．
5．已知a为实数，函数f（x）=x2-|x2-ax-2|在区间（-∞，-1）和（2，+∞）上单调递增，则a的取值范围为[1，8]．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网