��Ŀ����
7����ԲC��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0�����϶���ΪA��P��$\frac{4\sqrt{2}}{3}$��$\frac{b}{3}$����C�ϵ�һ�㣬��APΪֱ����Բ������ԲC���ҽ���F����1������ԲC�ķ��̣�
��2����ֱ��l��y=kx+m��|k|��$\frac{\sqrt{2}}{2}$������ԲC�ཻ��A��B���㣬MΪ��ԲC������һ�㣬���߶�OM���е����߶�AB���е��غϣ���|OM|��ȡֵ��Χ��
���� ��1��������APΪֱ����Բ������ԲC���ҽ���F���ɵ�$\overrightarrow{PF}•\overrightarrow{AF}$=0�����ɵ�P��$\frac{4\sqrt{2}}{3}$��$\frac{b}{3}$������Բ�ϣ������ɵ�a��b��c��ֵ������Բ���̿���
��2������ֱ�߷��̺���Բ���̣����A��B�е����꣬�õ�M���꣬��M���������Բ���̣��ɵ�m��k�Ĺ�ϵ����|OM|��Ϊ����k�Ĵ���ʽ�������֪k�ķ�Χ���|OM|��ȡֵ��Χ��
���  �⣺��1��A��0��b����
�⣺��1��A��0��b����
����APΪֱ����Բ������ԲC���ҽ���F����PF��AF��
��$\overrightarrow{PF}•\overrightarrow{AF}$=��c-$\frac{4\sqrt{2}}{3}$��-$\frac{b}{3}$��•��c��-b��=c��c-$\frac{4\sqrt{2}}{3}$��+$\frac{{b}^{2}}{3}$=0��
�ѵ�P��$\frac{4\sqrt{2}}{3}$��$\frac{b}{3}$��������ԲC��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��
��$\frac{32}{9{a}^{2}}+\frac{1}{9}=1$�����a2=4��
��b2+c2=4���ɵ�b2=4-c2������c��c-$\frac{4\sqrt{2}}{3}$��+$\frac{{b}^{2}}{3}=0$�����c=$\sqrt{2}$��b=$\sqrt{2}$��
����ԲC�ķ���Ϊ$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{2}=1$��
��2����ͼ����A��x1��y1����B��x2��y2����
����$\left\{\begin{array}{l}{y=kx+m}\\{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{2}=1}\end{array}\right.$���ã�1+2k2��x2+4kmx+2m2-4=0��
��=��4km��2-4��1+2k2����2m2-4��=32k2-8m2+16��0����4k2-m2+2��0 �٣�
${x}_{1}+{x}_{2}=\frac{-4km}{1+2{k}^{2}}$��
��${y}_{1}+{y}_{2}=k��{x}_{1}+{x}_{2}��+2m=k•\frac{-4km}{1+2{k}^{2}}+2m$=$\frac{2m}{1+2{k}^{2}}$��
��AB�е�G��$-\frac{2km}{1+2{k}^{2}}��\frac{m}{1+2{k}^{2}}$����
��M��$-\frac{4km}{1+2{k}^{2}}��\frac{2m}{1+2{k}^{2}}$����
��M����Բ$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{2}=1$�ϣ�
��$\frac{4{k}^{2}{m}^{2}}{��1+2{k}^{2}��^{2}}+\frac{2{m}^{2}}{��1+2{k}^{2}��^{2}}=1$�������ã�${m}^{2}=\frac{1+2{k}^{2}}{2}$��
��${m}^{2}=\frac{1+2{k}^{2}}{2}$����ٵã�$4{k}^{2}-\frac{1+2{k}^{2}}{2}+2��0$�������
��|OM|=$\sqrt{��-\frac{4km}{1+2{k}^{2}}��^{2}+��\frac{2m}{1+2{k}^{2}}��^{2}}$=$\sqrt{\frac{16{k}^{2}}{��1+2{k}^{2}��^{2}}•\frac{1+2{k}^{2}}{2}+\frac{4}{��1+2{k}^{2}��^{2}}•\frac{1+2{k}^{2}}{2}}$
=$\sqrt{\frac{8{k}^{2}+2}{2{k}^{2}+1}}$=$\sqrt{\frac{4��2{k}^{2}+1��-2}{2{k}^{2}+1}}=\sqrt{4-\frac{2}{2{k}^{2}+1}}$��
��|k|��$\frac{\sqrt{2}}{2}$����1��2k2+1��2����$4-\frac{2}{2{k}^{2}+1}��[2��3]$��
��|OM|��ȡֵ��ΧΪ$[\sqrt{2}��\sqrt{3}]$��
���� ���⿼������Բ�ı����̼������ʡ�ֱ������Բ�ཻ�ҳ����⣬������������֤�����������������������������˼�뷽�����������⣮

 ����ͼ���������������ϵ�д�
����ͼ���������������ϵ�д� ����ѧҵ���Ե�����ϵ�д�
����ѧҵ���Ե�����ϵ�д�| A�� | ��ֲ���Ҫ���� | B�� | ��Ҫ��������� | ||
| C�� | ��Ҫ���� | D�� | �Ȳ����Ҳ����Ҫ���� |
| A�� | ��ֲ���Ҫ | B�� | ��Ҫ����� | ||
| C�� | ��Ҫ | D�� | �Ȳ����Ҳ����Ҫ |
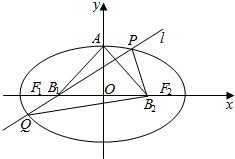 ��ͼ������Բ������Ϊԭ��O��������x���ϣ��϶���ΪA�����ҽ���ֱ�ΪF1��F2���߶�OF1��OF2���е�ֱ�ΪB1��B2���ҡ�AB1B2�����Ϊ1��ֱ�������Σ�
��ͼ������Բ������Ϊԭ��O��������x���ϣ��϶���ΪA�����ҽ���ֱ�ΪF1��F2���߶�OF1��OF2���е�ֱ�ΪB1��B2���ҡ�AB1B2�����Ϊ1��ֱ�������Σ� һ����������A��ȥB��ִ�������ȴ�A����ƫ��30�㷽����ʻ2ǧ��D�أ�Ȼ���D���ر�ƫ��60�㷽����ʻ6ǧ����C�أ���C��������ƫ��30�㷽����ʻ2ǧ�ײŵ���B�أ�
һ����������A��ȥB��ִ�������ȴ�A����ƫ��30�㷽����ʻ2ǧ��D�أ�Ȼ���D���ر�ƫ��60�㷽����ʻ6ǧ����C�أ���C��������ƫ��30�㷽����ʻ2ǧ�ײŵ���B�أ�