题目内容
5.已知函数f(x)=$\frac{\sqrt{3}}{2}$sin2x-cos2x-$\frac{1}{2}$(x∈R),设△ABC的内角A,B,C对应边分别为a,b,c,且c=$\sqrt{3}$,f(C)=0.(1)求C的值.
(2)若向量$\overrightarrow{m}$=(1,sinA)与向量$\overrightarrow{n}$=(2,sinB)共线,求△ABC的面积.
分析 (1)利用三角函数恒等变换的应用化简可得函数解析式为:f(x)=sin(2x-$\frac{π}{6}$)-1,由f(C)=0得sin(2C-$\frac{π}{6}$)=1,结合范围-$\frac{π}{6}$<2C-$\frac{π}{6}$<$\frac{11π}{6}$,即可解得C的值.
(2)利用向量共线可得2sinA=sinB,由正弦定理可得b=2a,由余弦定理得a2+b2-ab=3,联立解得a,b的值,利用三角形面积公式即可求值得解.
解答 解:(1)∵f(x)=$\frac{\sqrt{3}}{2}$sin2x-cos2x-$\frac{1}{2}$,…(1分)
f(x)=sin(2x-$\frac{π}{6}$)-1,…(2分)
由f(C)=0得sin(2C-$\frac{π}{6}$)=1,…(3分)
又∵-$\frac{π}{6}$<2C-$\frac{π}{6}$<$\frac{11π}{6}$,…(4分)
∴2C-$\frac{π}{6}$=$\frac{π}{2}$,…(5分)
即C=$\frac{π}{3}$…(6分)
(2)∵向量$\overrightarrow{m}$=(1,sinA)与向量$\overrightarrow{n}$=(2,sinB)共线,
∴2sinA=sinB,…(7分)
∴b=2a,①…(8分)
由余弦定理,得a2+b2-ab=3,②…(9分)
∴由①②得:a=1,b=2…(10分)
∴△ABC的面积为$\frac{1}{2}$absinC=$\frac{\sqrt{3}}{2}$.…(12分)
点评 本题主要考查了三角函数恒等变换的应用,正弦定理,余弦定理,三角形面积公式,平面向量数量积的运算,考查了计算能力和转化思想,属于中档题.

| A. | A?B | B. | B⊆A | C. | A=B | D. | A∩B=∅ |
| A. | y=x3 | B. | y=2x2-3 | C. | y=x | D. | y=x2,x∈[0,1] |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
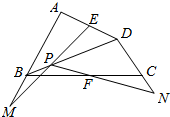 如图,四边形ABCD中,E,F分别是AD,BC的中点,P是对角线BD上的一点,直线EP,PF分别交AB,DC的延长线于M,N.证明:线段MN被直线EF所平分.
如图,四边形ABCD中,E,F分别是AD,BC的中点,P是对角线BD上的一点,直线EP,PF分别交AB,DC的延长线于M,N.证明:线段MN被直线EF所平分.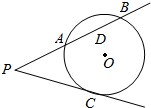 如图,过点P作圆O的切线PC,切点为C,过点P的直线与圆O交于点A,B(PA<PB),且AB的中点为D.
如图,过点P作圆O的切线PC,切点为C,过点P的直线与圆O交于点A,B(PA<PB),且AB的中点为D.