题目内容
11. 如图,网格纸上小正方形的边长为1,实线画出的是某多面体的三视图,则该多面体的体积为( )
如图,网格纸上小正方形的边长为1,实线画出的是某多面体的三视图,则该多面体的体积为( )| A. | 20 | B. | 22 | C. | 24 | D. | 26 |
分析 由三视图可知:该几何体是一个棱长为3正方体去掉3个棱长为1的小正方体剩下的部分.
解答 解:由三视图可知:该几何体是一个棱长为3正方体去掉3个棱长为1的小正方体剩下的部分.
该几何体的体积V=33-3×13
=24.
故选:C.
点评 本题考查了正方体的三视图、体积计算公式,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目
1.某四棱锥的三视图如图所示,则它的外接球的表面积为( )
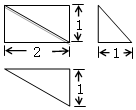

| A. | 6π | B. | 24π | C. | 4π | D. | 36π |
3.曲线y=x${\;}^{\frac{1}{2}}$与y=x2所围成的封闭区域的面积为( )
| A. | $\frac{1}{3}$ | B. | $\frac{5}{12}$ | C. | $\frac{4}{5}$ | D. | $\frac{5}{2}$ |
1.函数f(x)=sin(ωx+φ),(|φ|<$\frac{π}{2}$)的部分图象如图所示,则f(x)的单调递增区间为( )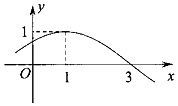

| A. | (-1+4kπ,1+4kπ),k∈Z | B. | (-3+8kπ,1+8kπ),k∈Z | ||
| C. | (-1+4k,1+4k),k∈Z | D. | (-3+8k,1+8k),k∈Z |
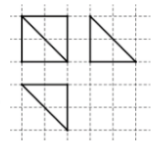 如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则此几何体各面直角三角形的个数是( )
如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则此几何体各面直角三角形的个数是( )