题目内容

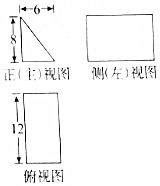
1．某四棱锥的三视图如图所示，则它的外接球的表面积为（　　）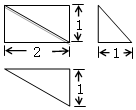
A．6πB．24πC．4πD．36π

分析 由已知可得四棱锥的外接球相当于一个长，宽，高分别为：2，1，1的长方体的外接球，进而得到答案．

解答 解：由已知可得四棱锥是以主视图为底面的，
其外接球相当于一个长，宽，高分别为：2，1，1的长方体的外接球，
其外接球直径R=$\frac{\sqrt{{1}^{2}+{2}^{2}+{1}^{2}}}{2}$=$\frac{\sqrt{6}}{2}$，
故它的外接球的表面积S=4πR2=6π，
故选：A

点评 本题考查的知识点是球内接多面体，球的体积与表面积，简单几何体的三视图，难度中档．

练习册系列答案
相关题目
11．已知数列{an}的前n项和为Sn，且满足4nSn=（n+1）2an．a1=1
（1）求an；
（2）设bn=$\frac{n}{{a}_{n}}$，数列{bn}的前n项和为Tn，求证：Tn＜$\frac{7}{4}$．
12．设向量$\overrightarrow{a}$=（cosx，-sinx），$\overrightarrow{b}$=（-cos（$\frac{π}{2}$-x），cosx），且$\overrightarrow{a}$=t$\overrightarrow{b}$，t≠0，则sin2x的值等于（　　）
A．1B．-1C．±1D．0
9．定义：二阶行列式$|\begin{array}{l}{a}&{b}\\{c}&{d}\end{array}|$=ad-bc（a，b，c，d∈R）．已知数列{an}满足a1=1，a2=2，$|\begin{array}{l}{{a}_{n+2}}&{{a}_{n+1}}\\{{a}_{n+1}}&{{a}_{n}}\end{array}|$=（-1）n+1（n∈N*）．
（Ⅰ）求a3，a4，a5；
（Ⅱ）求证：an+2=2an+1+an（n∈N*）
（Ⅲ）试问该数列任意两个相邻项的平方和仍然是该数列中的一个项吗？如果是，请证明你的结论；如果不是，请说明理由．
16．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）经过点（$\sqrt{2}$，1），过点A（0，1）的动直线l与椭圆C交于M、N两点，当直线l过椭圆C的左焦点时，直线l的斜率为$\frac{\sqrt{2}}{2}$．
（1）求椭圆C的方程；
（2）是否存在与点A不同的定点B，使得∠ABM=∠ABN恒成立？若存在，求出点B的坐标；若不存在，请说明理由．
6．已知点P（0，-2），点A，B分别为椭圆E：$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1（a＞b＞0）的左右顶点，直线BP交E于点Q，△ABP是等腰直角三角形，且$\overrightarrow{PQ}$=$\frac{3}{2}\overrightarrow{QB}$．
（1）求E的方程；
（2）设过点的动直线l与E相交于M，N两点，当坐标原点O位于MN以为直径的圆外时，求直线l斜率的取值范围．
13．一个几何体的三视图如图所示，则这个几何体的外接球的半径为$\sqrt{61}$．
10．已知袋子中放有大小和形状相同的小球若干，其中标号为0的小球1个，标号为1的小球1个，标号为2的小球n个．若从袋子中随机抽取1个小球，取到标号为2的小球的概率是$\frac{1}{2}$．
（1）求n的值；
（2）从袋子中不放回地随机抽取2个小球，记第一次取出的小球标号为a，第二次取出的小球标号为b．
（i）记“a+b=2”为事件A，求事件A的概率；
（ii）在区间[0，2]内任取2个实数x，y，求事件“x2+y2＞（a-b）2恒成立”的概率．
11．如图，网格纸上小正方形的边长为1，实线画出的是某多面体的三视图，则该多面体的体积为（　　）
A．20B．22C．24D．26

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网