题目内容

20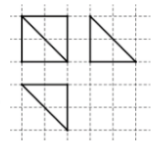．如图，网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图，则此几何体各面直角三角形的个数是（　　）
A．2B．3C．4D．5

分析 由三视图可知：该几何体为四棱锥P-ABCD，侧面PAD⊥底面ABCD，PA⊥AD，底面ABCD是正方形．即可得出．

解答 解：由三视图可知：该几何体为四棱锥P-ABCD，侧面PAD⊥底面ABCD，PA⊥AD，底面ABCD是正方形．
则此图中含有4个直角三角形（除了底面正方形）．
故选：C．

点评 本题考查了四棱锥的三视图、线面面面垂直的判定与性质定理，考查了推理能力与计算能力，属于基础题．

练习册系列答案
相关题目
10．已知袋子中放有大小和形状相同的小球若干，其中标号为0的小球1个，标号为1的小球1个，标号为2的小球n个．若从袋子中随机抽取1个小球，取到标号为2的小球的概率是$\frac{1}{2}$．
（1）求n的值；
（2）从袋子中不放回地随机抽取2个小球，记第一次取出的小球标号为a，第二次取出的小球标号为b．
（i）记“a+b=2”为事件A，求事件A的概率；
（ii）在区间[0，2]内任取2个实数x，y，求事件“x2+y2＞（a-b）2恒成立”的概率．
11．如图，网格纸上小正方形的边长为1，实线画出的是某多面体的三视图，则该多面体的体积为（　　）
A．20B．22C．24D．26
8．若正数x，y满足15x-y=22，则x3+y3-x2-y2的最小值为1．
15．以直角坐标系的原点O为极点，x轴的正半轴为极轴建立极坐标系，已知点M的直角坐标为（1，0），若直线l的极坐标方程为$\sqrt{2}$ρcos（θ+$\frac{π}{4}$）-1=0，曲线C的参数方程是$\left\{\begin{array}{l}{x=4{t}^{2}}\\{y=4t}\end{array}\right.$（t为参数）．
（1）求直线l和曲线C的普通方程；
（2）设直线l与曲线C交于A，B两点，求$\frac{1}{|MA|}$+$\frac{1}{|MB|}$．
5．已知正三角形ABC的三个顶点都在球心为O、半径为3的球面上，且三棱锥O-ABC的高为2，点D是线段BC的中点，过点D作球O的截面，则截面积的最小值为（　　）
A．$\frac{15π}{4}$B．4πC．$\frac{7π}{2}$D．3π
12．已知一个几何体的三视图如图所示，则该几何体的表面积为（　　）
A．4$\sqrt{2}$+6B．4$\sqrt{2}$+8C．4$\sqrt{2}$+12D．4$\sqrt{2}$+10
9．三棱锥S-ABC的所有顶点都在球O的表面上，SA⊥平面ABC，AB⊥AC，又SA=AB=AC=1，则球O的表面积为（　　）
A．$\frac{{\sqrt{3}}}{2}π$B．$\frac{3}{2}π$C．3πD．12π
10．在平面区域$\left\{\begin{array}{l}{x+y-4≤0}\\{x＞0}\\{y＞0}\end{array}\right.$内随机取一点（a，b），则函数f（x）=ax2-4bx+1在区间[1，+∞）上是增函数的概率为（　　）
A．$\frac{1}{4}$B．$\frac{1}{3}$C．$\frac{1}{2}$D．$\frac{2}{3}$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网