题目内容
6.意大利数学家列昂那多•斐波那契以兔子繁殖为例,引入“兔子数列”:1,1,2,3,5,8,13,21,34,55,89,144,233,…,即F(1)=F(2)=1,F(n)=F(n-1)+F(n-2)(n≥3,n∈N*),此数列在现代物理、准晶体结构、化学等领域都有着广泛的应用,若此数列被3整除后的余数构成一个新数列{bn},b2017=1.分析 由题意可得数列从第三项开始,后一项为前两项的和,再分别除以3得到一个新的数列,该数列的周期为8,即可求出答案.
解答 解:1,1,2,3,5,8,13,21,34,55,89,144,233,377,…,
此数列被3整除后的余数构成一个新数列{bn},
则{bn},1,1,2,0,2,2,1,0,1,1,2,0,2,2,…,
其周期为8,
故b2017=b227×8+1=b1=1,
故答案为:1
点评 本题考查数列的概念及简单表示法,考查推理与运算能力,属于中档题.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
11. 如图,网格纸上小正方形的边长为1,实线画出的是某多面体的三视图,则该多面体的体积为( )
如图,网格纸上小正方形的边长为1,实线画出的是某多面体的三视图,则该多面体的体积为( )
 如图,网格纸上小正方形的边长为1,实线画出的是某多面体的三视图,则该多面体的体积为( )
如图,网格纸上小正方形的边长为1,实线画出的是某多面体的三视图,则该多面体的体积为( )| A. | 20 | B. | 22 | C. | 24 | D. | 26 |
16.设复数z满足z(2+i)=5i,则|z-1|=( )
| A. | 1 | B. | 2 | C. | $\sqrt{3}$ | D. | 5 |
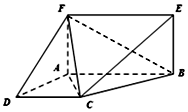 如图,已知AF⊥平面ABCD,四边形ABEF为矩形,四边形ABCD为直角梯形,∠DAB=90°,AB∥CD,AD=AF=CD=2,AB=4.
如图,已知AF⊥平面ABCD,四边形ABEF为矩形,四边形ABCD为直角梯形,∠DAB=90°,AB∥CD,AD=AF=CD=2,AB=4.