题目内容
8.已知等比数列{an}各项都为正数,且满足a2=2,a6=6,a4=( )| A. | 4 | B. | 8 | C. | $\sqrt{3}$ | D. | 2$\sqrt{3}$ |
分析 利用等比数列的性质即可得出.
解答 解:等比数列{an}各项都为正数,
利用等比数列的性质可得:${a}_{4}=\sqrt{{a}_{2}{a}_{6}}$=$\sqrt{2×6}$=2$\sqrt{3}$.
故选:D.
点评 本题考查了等比数列的性质,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
2.已知函数f(x)=a-x+xex,若存在x0>-1,使得f(x0)≤0,则实数a的取值范围为( )
| A. | [0,+∞) | B. | (-∞,0] | C. | [1,+∞) | D. | (-∞,1] |
3.有一种细胞每半小时分裂一次,由原来的一个分裂成两个,那么一个这种细胞经过3小时分裂成的细胞数为( )
| A. | 32 | B. | 64 | C. | 128 | D. | 254 |
20.一椭圆的两个焦点坐标分别为F1(0,-8),F2(0,8),且椭圆上的一点到两个焦点的距离之和为20,则此椭圆的标准方程为( )
| A. | $\frac{x^2}{100}$+$\frac{y^2}{36}$=1 | B. | $\frac{y^2}{400}$+$\frac{x^2}{336}$=1 | C. | $\frac{y^2}{100}$+$\frac{x^2}{36}$=1 | D. | $\frac{y^2}{20}$+$\frac{x^2}{12}$=1 |
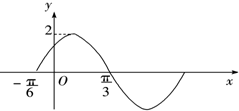 函数f1(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的一段图象如图所示.
函数f1(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的一段图象如图所示.