题目内容
5.已知{an}为等差数列,{bn}为正项等比数列,公比q≠1,若a1=b1,a13=b13,则( )| A. | a7=b7 | B. | a7>b7 | C. | a7<b7 | D. | a7>b7或a7<b7 |
分析 由已知条件推导出a7=$\frac{{a}_{1}+{a}_{13}}{2}$,b7=$\sqrt{{b}_{1}{b}_{13}}$,由基本不等式可知a7>b7.
解答 解:∵{an}为等差数列,
∴a7=$\frac{{a}_{1}+{a}_{13}}{2}$,
∵{bn}为正项等比数列,
∴b7=$\sqrt{{b}_{1}{b}_{13}}$,公比q≠1,
∵a1=b1,a13=b13,
由基本不等式可知a7>b7,
故选B.
点评 本题考查两数大小的比较,是基础题,解题时要认真审题,注意基本不等式性质的合理运用.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案
相关题目
20.一椭圆的两个焦点坐标分别为F1(0,-8),F2(0,8),且椭圆上的一点到两个焦点的距离之和为20,则此椭圆的标准方程为( )
| A. | $\frac{x^2}{100}$+$\frac{y^2}{36}$=1 | B. | $\frac{y^2}{400}$+$\frac{x^2}{336}$=1 | C. | $\frac{y^2}{100}$+$\frac{x^2}{36}$=1 | D. | $\frac{y^2}{20}$+$\frac{x^2}{12}$=1 |
15.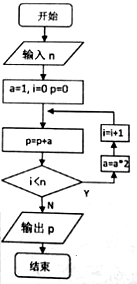 要使如图所示的程序框图输出的P不小于60,则输入的n值至少为( )
要使如图所示的程序框图输出的P不小于60,则输入的n值至少为( )
 要使如图所示的程序框图输出的P不小于60,则输入的n值至少为( )
要使如图所示的程序框图输出的P不小于60,则输入的n值至少为( )| A. | 5 | B. | 6 | C. | 7 | D. | 4 |
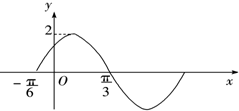 函数f1(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的一段图象如图所示.
函数f1(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的一段图象如图所示. 已知函数f(x)=$\left\{\begin{array}{l}{{2}^{x}-2,x≥0}\\{-2x+1,x<0}\end{array}\right.$,
已知函数f(x)=$\left\{\begin{array}{l}{{2}^{x}-2,x≥0}\\{-2x+1,x<0}\end{array}\right.$,