题目内容
一个口袋中装有m个白球,n个黑球,从口袋中每次拿一个球不放回,第k次拿到黑球的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:相互独立事件的概率乘法公式
专题:计算题,概率与统计
分析:不管什么时候拿,白球黑球概率都一样,也就是可能拿到白球,也能拿到黑球,即可得出结论.
解答:
解:不管什么时候拿,白球黑球概率都一样,也就是可能拿到白球,也能拿到黑球,
k次时,拿了(k-1)个球,(k-1)球中白球比黑球=m比n,剩下的(m+n-k+1)个球中白球比黑球=m比n,
所以第k次拿到黑球的概率是
.
故选:C.
k次时,拿了(k-1)个球,(k-1)球中白球比黑球=m比n,剩下的(m+n-k+1)个球中白球比黑球=m比n,
所以第k次拿到黑球的概率是
| n |
| m+n |
故选:C.
点评:本题考查概率的计算,考查学生分析解决问题的能力,比较基础.

练习册系列答案
相关题目
若函数f(x)=
(a,b,c,d∈R)的图象如图所示,则a:b:c:d=( )
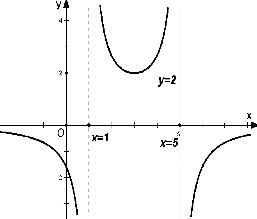
| d |
| ax2+bx+c |

| A、1:6:5:8 |
| B、1:6:5:(-8) |
| C、1:(-6):5:8 |
| D、1:(-6):5:(-8) |
独立性检验,适用于检查( )变量之间的关系.
| A、线性 | B、非线性 |
| C、解释与预报 | D、分类 |
设直线y=t与函数f(x)=x
,g(x)=ex的图象分别交于点M,N,则当|MN|达到最小时t的值为( )
| 1 |
| 2 |
| A、1 | ||||
B、
| ||||
C、
| ||||
D、
|
与圆x2+y2-4y=0外切,又与x轴相切的圆的圆心轨迹方程是( )
| A、y2=8x |
| B、y2=8x(x>0)和y=0 |
| C、x2=8y(y>0) |
| D、x2=8y(y>0)和x=0(y<0) |
用反证法证明:某方程“方程有唯一解”中,假设正确的是该方程( )
| A、无解 | B、有两个解 |
| C、至少两解 | D、至少有两个解或无解 |
不等式x2-3x-10<0的解集为( )
| A、{x|2<x<5} |
| B、{x|-5<x<2} |
| C、{x|-2<x<5} |
| D、{x|-5<x<-2} |
已知函数f(x)=
cosx,则f′(
)=( )
| 1 |
| x |
| π |
| 2 |
A、-
| ||
B、
| ||
C、
| ||
D、-
|
已知数列{an},满足a1=1,an=3-an-1(n∈N*,n≥2),则a2014=( )
| A、1 | B、2 |
| C、2014 | D、2015 |