题目内容
数列{an}中,已知对任意n∈N*,a1+a2+a3+…+an=3n-1,则 +
+ +
+ +…+
+…+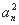 等于( )
等于( )
(A)(3n-1)2 (B) (9n-1)
(9n-1)
(C)9n-1 (D) (3n-1)
(3n-1)
B
解析:已知a1+a2+a3+…+an=3n-1,①
当n≥2时,a1+a2+…+an-1=3n-1-1,②
由①-②得an=(3n-1)-(3n-1-1)=2·3n-1,
∴{an}是首项为2,公比为3的等比数列.
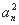 =(2·3n-1)2=4·32n-2=4·9n-1,
=(2·3n-1)2=4·32n-2=4·9n-1,
∴{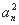 }是首项为4,公比为9的等比数列,
}是首项为4,公比为9的等比数列,
故 +
+ +…+
+…+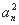 =
= =
= (9n-1).
(9n-1).

练习册系列答案
 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
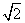 C.2 D.2
C.2 D.2 的前5项和为( )
的前5项和为( ) (B)
(B) (C)
(C)  (D)
(D)
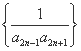 的前n项和.
的前n项和.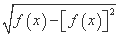 +
+ 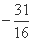 ,则f(15)= .
,则f(15)= .  ,则f(-1)等于( )
,则f(-1)等于( )