题目内容
若以椭圆上一点和两个焦点为顶点的三角形面积的最大值为1,则椭圆长轴长的最小值为( )
A.1 B.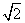 C.2 D.2
C.2 D.2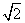
D

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
题目内容
若以椭圆上一点和两个焦点为顶点的三角形面积的最大值为1,则椭圆长轴长的最小值为( )
A.1 B.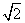 C.2 D.2
C.2 D.2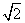
D

 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案