题目内容
对任意x∈R,函数f(x)满足f(x+1)= 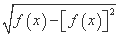 +
+  ,设an=[f(n)]2-f(n),数列{an}的前15项的和为
,设an=[f(n)]2-f(n),数列{an}的前15项的和为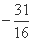 ,则f(15)= .
,则f(15)= .
 解析:因为f(x+1)=
解析:因为f(x+1)= 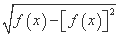 +
+  ,
,
所以f(x+1)-  =
=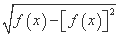 ≥0,
≥0,
即f(x+1)≥ .
.
两边平方得[f(x+1)-  ]2=f(x)-[f(x)]2,
]2=f(x)-[f(x)]2,
即[f(x+1)]2-f(x+1)+  =f(x)-[f(x)]2,
=f(x)-[f(x)]2,
即[f(x+1)]2-f(x+1)+[f(x)]2-f(x)=-  ,
,
即an+1+an=- ,
,
即数列{an}的任意相邻两项之和为- ,
,
所以S15=7×(- )+a15=-
)+a15=- ,即a15=-
,即a15=- .
.
所以a15=[f(15)]2-f(15)=- ,
,
解得f(15)= 或f(15)=
或f(15)= (舍去).
(舍去).

练习册系列答案
相关题目
 +
+ +
+ +…+
+…+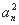 等于( )
等于( )

 或-
或-