题目内容
与双曲线
-y2=1有共同渐近线且经过点(2,-2)的双曲线的方程为 .
| x2 |
| 2 |
考点:双曲线的标准方程
专题:圆锥曲线的定义、性质与方程
分析:由双曲线有共同渐近线的特点设出双曲线的方程为
-y2=λ(λ≠0),把点(2,-2)代入求出λ再化简即可.
| x2 |
| 2 |
解答:
解:由题意设所求的双曲线的方程为
-y2=λ(λ≠0),
因为经过点(2,-2),所以2-4=λ,即λ=-2,
代入方程化简得,
-
=1,
故答案为:
-
=1.
| x2 |
| 2 |
因为经过点(2,-2),所以2-4=λ,即λ=-2,
代入方程化简得,
| y2 |
| 2 |
| x2 |
| 4 |
故答案为:
| y2 |
| 2 |
| x2 |
| 4 |
点评:本题考查双曲线特有的性质:渐近线,熟练掌握双曲线有共同渐近线的方程特点是解题的关键.

练习册系列答案
相关题目
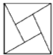 如图,大正方形的面积是13,四个全等的直角三角形围成一个小正方形,直角三角形的较短边长为2,向大正方形内投一飞镖,则飞镖落在小正方形内的概率为
如图,大正方形的面积是13,四个全等的直角三角形围成一个小正方形,直角三角形的较短边长为2,向大正方形内投一飞镖,则飞镖落在小正方形内的概率为