题目内容
8.已知函数f(x)=3klnx+$\frac{2{k}^{2}-{x}^{2}}{x}$(k为常数,k>0).(1)当k=1时,求f(x)的极值;
(2)若k∈[3,+∞),曲线y=f(x)上总存在相异两点M(x1,y1),N(x2,y2),使得曲线y=f(x)在M,N两点处的切线互相平行,求x1+x2的取值范围.
分析 (1)求出函数的导数,解关于导函数的不等式,求出函数的单调区间,从而求出函数的极值;
(2)求出函数的导数,根据f′(x1)=f′(x2),得到x1+x2=$\frac{3}{2k}$x1x2,结合不等式的基本性质,求出其范围即可.
解答 解:(1)k=1时,f(x)=3lnx-x+$\frac{2}{x}$,(x>0),
f′(x)=-$\frac{(x-1)(x-2)}{x}$,
令f′(x)>0,解得:1<x<2,令f′(x)<0,解得:0<x<1或x>2,
∴f(x)在(0,1)递减,在(1,2)递增,在(2,+∞)递减,
∴f(x)极小值=f(1)=1,f(x)极大值=f(2)=3ln2-1;
(2)∵f′(x)=$\frac{3k}{x}$-1-$\frac{{2k}^{2}}{{x}^{2}}$,k∈[3,+∞),
由题意,可得f′(x1)=f′(x2)(x1,x2>0,且x1≠x2),
∴$\frac{3k}{{x}_{1}}$-1-$\frac{{2k}^{2}}{{{x}_{1}}^{2}}$=$\frac{3k}{{x}_{2}}$-1-$\frac{{2k}^{2}}{{{x}_{2}}^{2}}$,
∴x1+x2=$\frac{3}{2k}$x1x2≤$\frac{3}{2k}$${(\frac{{x}_{1}{+x}_{2}}{2})}^{2}$,
∴x1+x2>$\frac{8k}{3}$≥8,
故x1+x2的取值范围是(8,+∞).
点评 本题考查了函数的单调性、极值问题,考查导数的应用以及不等式的性质,是一道中档题.

练习册系列答案
相关题目
18.为了解某地区观众对大型综艺活动《中国好声音》的收视情况,随机抽取了100名观众进行调查,其中女性有55名.下面是根据调查结果绘制的观众收看该节目的场数与所对应的人数表:
将收看该节目场次不低于13场的观众称为“歌迷”,已知“歌迷”中有10名女性.
根据已知条件完成下面的2×2列联表,并据此资料判断我们能否有95%的把握认为“歌迷”与性别有关?
附:
${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d为样本容量.
| 场数 | 9 | 10 | 11 | 12 | 13 | 14 |
| 人数 | 10 | 18 | 22 | 25 | 20 | 5 |
根据已知条件完成下面的2×2列联表,并据此资料判断我们能否有95%的把握认为“歌迷”与性别有关?
| 非歌迷 | 歌迷 | 合计 | |
| 男 | |||
| 女 | |||
| 合计 |
| P(K2≥k0) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
3.若{1,a,$\frac{b}{a}$}={0,a2,a+b},则a2009+b2009的值为( )
| A. | 0 | B. | 1 | C. | -1 | D. | 1或-1 |
13.已知曲线C的参数方程为$\left\{{\begin{array}{l}{x=1+3t}\\{y=a{t^2}+2}\end{array}}$(t为参数,a∈R),点M(4,3)在曲线C上,则a=( )
| A. | -2 | B. | 0 | C. | 1 | D. | 2 |
17.已知偶函数f(x)在[0,π]上单调递增,那么下列各式正确的是( )
| A. | f(-π)>f(log2$\frac{1}{4}$)>f($-\frac{π}{2}$) | B. | f(log2$\frac{1}{4}$)>f(-$\frac{π}{2}$)>f(-π) | ||
| C. | f(-π)>f(-$\frac{π}{2}$)>f(log2$\frac{1}{4}$) | D. | f(-$\frac{π}{2}$)>f(log2$\frac{1}{4}$)>f(-π) |
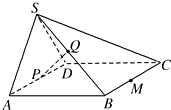 如图,在四棱锥S-ABCD中,平面SAD⊥平面ABCD,四边形ABCD为正方形,且P为AD的中点,Q为SB的中点.
如图,在四棱锥S-ABCD中,平面SAD⊥平面ABCD,四边形ABCD为正方形,且P为AD的中点,Q为SB的中点.