题目内容
4．已知点F，A是椭圆C：$\frac{x^2}{16}+\frac{y^2}{12}=1$的左焦点和上顶点，若点P是椭圆C上一动点，则△PAF周长的最大值为16．分析 根据椭圆的定义，丨PF丨+丨PF2丨=2a=8，丨AF丨+丨AF2丨=2a=8，则l=丨AF丨+丨PF丨+丨PA丨≤丨AF丨+丨PF丨+丨PF2丨+丨AF2丨=4a=16，即可求得△PAF周长的最大值．
解答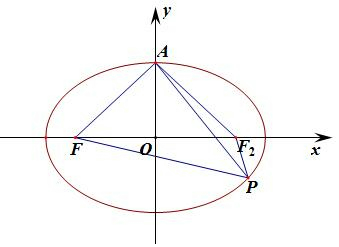 
解：椭圆C：$\frac{x^2}{16}+\frac{y^2}{12}=1$，a=4，b=2$\sqrt{2}$，c=2，则左焦点（-2，0）和上顶点（0，2$\sqrt{2}$），
则椭圆的右焦点F2（-2，0），
由椭圆的定义丨PF丨+丨PF2丨=2a=8，丨AF丨+丨AF2丨=2a=8，
∴△PAF周长l：l=丨AF丨+丨PF丨+丨PA丨≤丨AF丨+丨PF丨+丨PF2丨+丨AF2丨=4a=16，
当且仅当AP过F2时△PAF周长取最大值，
∴△PAF周长的最大值16，
故答案为：16．
点评 本题考查椭圆的性质及椭圆的定义，考查计算能力，考查数形结合思想，属于中档题．
练习册系列答案
相关题目
14．若$cos（α-\frac{π}{3}）=\frac{2}{3}$，α是锐角，则sinα=（ ）
| A． | $\frac{{\sqrt{15}}}{6}$ | B． | $\frac{{\sqrt{5}-\sqrt{3}}}{6}$ | C． | $\frac{{2\sqrt{3}-\sqrt{5}}}{6}$ | D． | $\frac{{4-\sqrt{15}}}{6}$ |
15．在长为8cm的线段AB上任取一点C，作一矩形，邻边长分别等于线段AC，CB的长，则该矩形面积小于15cm2的概率为（ ）
| A． | $\frac{8}{15}$ | B． | $\frac{3}{5}$ | C． | $\frac{3}{4}$ | D． | $\frac{2}{3}$ |
12．已知$|{\overrightarrow a}|=1$，$\overrightarrow a$与$\overrightarrow b$的夹角为$\frac{π}{3}$，$（{\overrightarrow a+2\overrightarrow b}）•\overrightarrow a=3$，则$|{\overrightarrow b}|$的值是（ ）
| A． | 3 | B． | 1 | C． | $\sqrt{2}$ | D． | 2 |
9．双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的右焦点到该双曲线渐近线的距离等于（ ）
| A． | a | B． | b | C． | $\sqrt{ab}$ | D． | $\frac{a+b}{2}$ |
16．已知双曲线过点（2，3），其中一条渐近线方程为$y=\sqrt{3}x$，则双曲线的标准方程是（ ）
| A． | $\frac{{7{x^2}}}{16}-\frac{y^2}{12}=1$ | B． | $\frac{y^2}{3}-\frac{x^2}{2}=1$ | C． | ${x^2}-\frac{y^2}{3}=1$ | D． | $\frac{{3{y^2}}}{23}-\frac{x^2}{23}=1$ |