题目内容
11.在体积为V的平行六面体ABCD-A1B1C1D1中,P为其内一动点(包括表面),若$\overrightarrow{AP}$=x$\overrightarrow{AB}$+y$\overrightarrow{AD}$+z$\overrightarrow{A{A}_{1}}$,且x+y+z≤1,则点P所有的位置构成的几何体的体积是$\frac{1}{6}$V.分析 设平行六面体ABCD-A1B1C1D1的底面平行四边形ABCD的面积为S,高为h,可得V=Sh.由于P为平行六面体ABCD-A1B1C1D1中内一动点(包括表面),$\overrightarrow{AP}$=x$\overrightarrow{AB}$+y$\overrightarrow{AD}$+z$\overrightarrow{A{A}_{1}}$,且x+y+z≤1,可得点P所有的位置构成的几何体是三棱锥A1-ABD.即可得出.
解答 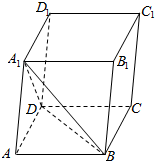 解:如图所示,
解:如图所示,
设平行六面体ABCD-A1B1C1D1的底面平行四边形ABCD的面积为S,高为h,
则V=Sh.
P为平行六面体ABCD-A1B1C1D1中内一动点(包括表面),$\overrightarrow{AP}$=x$\overrightarrow{AB}$+y$\overrightarrow{AD}$+z$\overrightarrow{A{A}_{1}}$,且x+y+z≤1,
∴点P所有的位置构成的几何体是三棱锥A1-ABD.
∴三棱锥A1-ABD的体积=$\frac{1}{3}{S}_{△ABD}$•h=$\frac{1}{3}×\frac{1}{2}S$•h=$\frac{1}{6}$V.
故答案为:$\frac{1}{6}$V.
点评 本题考查了平行四面体的性质、三棱锥的体积、空间向量的运算性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.给出下列命题,①在空间中,若$\overrightarrow{a}$=λ$\overrightarrow{b}$(λ∈R),则$\overrightarrow{a}$∥$\overrightarrow{b}$:②在空间中,$\overrightarrow{a}$∥$\overrightarrow{b}$,则$\overrightarrow{a}$=λ$\overrightarrow{b}$(λ∈R),下列说法正确的是( )
| A. | ①是真命题,②是假命题 | B. | ①是假命题,②是真命题 | ||
| C. | ①②都是真命题 | D. | ①②都是假命题 |
2.已知a=1.7-2.5,b=2.51.7,c=${log_2}{\frac{2}{3}}$,则a,b,c的大小关系为( )
| A. | a<b<c | B. | b<a<c | C. | c<b<a | D. | c<a<b |
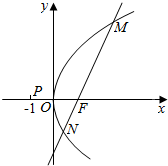 已知点F为抛物线C:y2=2px(p>0)的焦点,过点F的动直线l与抛物线C交于M,N两点,如图.当直线l与x轴垂直时,|MN|=4.
已知点F为抛物线C:y2=2px(p>0)的焦点,过点F的动直线l与抛物线C交于M,N两点,如图.当直线l与x轴垂直时,|MN|=4.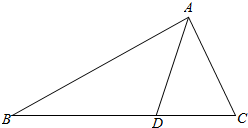 如图,在△ABC中,点D在BC边上,∠CAD=$\frac{π}{4}$,AC=$\frac{7}{2}$,cos∠ADB=-$\frac{{\sqrt{2}}}{10}$.
如图,在△ABC中,点D在BC边上,∠CAD=$\frac{π}{4}$,AC=$\frac{7}{2}$,cos∠ADB=-$\frac{{\sqrt{2}}}{10}$.