题目内容
过点(1,2)且与直线3x-2y-1=0平行的直线方程是( )
| A、3x-2y+1=0 |
| B、2x-3y+1=0 |
| C、3x-2y+2=0 |
| D、2x-3y+2=0 |
考点:直线的一般式方程与直线的平行关系
专题:直线与圆
分析:由直线的平行关系可设方程为3x-2y+c=0,代已知点可得c值,可得方程.
解答:
解:由题意设所求直线的方程为3x-2y+c=0,
∵直线过点(1,2),
∴3×1-2×2+c=0,
解得c=1,∴直线方程为3x-2y+1=0
故选:A
∵直线过点(1,2),
∴3×1-2×2+c=0,
解得c=1,∴直线方程为3x-2y+1=0
故选:A
点评:本题考查直线的一般式方程,涉及直线的平行关系,属基础题.

练习册系列答案
相关题目
如图所示的程序框图,输出S的值是
,则判断框内应填( )

| 1 |
| 2016 |

| A、n<2015? |
| B、n≤2014? |
| C、n≤2016? |
| D、n≤2015? |
 如图,边长为2的正方形内有一个椭圆,用随机模拟的方法估计该椭圆的面积,在正方形中随机撒了10000粒豆子,落在椭圆内的有8000粒,据此估计该椭圆的面积为( )
如图,边长为2的正方形内有一个椭圆,用随机模拟的方法估计该椭圆的面积,在正方形中随机撒了10000粒豆子,落在椭圆内的有8000粒,据此估计该椭圆的面积为( )| A、3.14 | B、3.2 |
| C、12.56 | D、12.8 |
在如图的程序图中,输出结果是( )


| A、5 | B、10 | C、20 | D、15 |
一质点沿直线运动,若由始点起经过t秒后的位移为s=
t3+
t2-4t+7,那么速度为0的时刻为( )
| 1 |
| 3 |
| 3 |
| 2 |
| A、0秒 | B、1秒末 |
| C、2秒末 | D、1秒末和2秒末 |
已知F是抛物线y2=2x的焦点,A,B是该抛物线上的两点,|AF|+|BF|=3,则线段AB的中点到y轴的距离为( )
A、
| ||
| B、1 | ||
C、
| ||
D、
|
x,y∈R,x∈[0,1],y∈[0,1],则x2≤y≤x的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
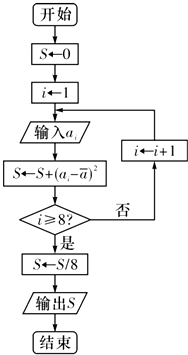 对一个作直线运动的质点的运动过程观测了8次,得到如表所示的数据.
对一个作直线运动的质点的运动过程观测了8次,得到如表所示的数据. “幸福感指数”是指某个人主观地评价他对自己目前生活状态的满意程度时,给出的区间内的一个数,该数越接近10表示越满意,为了解某大城市市民的幸福感,随机对该城市的男、女各500人市民进行了调查,调查数据如下表所示:
“幸福感指数”是指某个人主观地评价他对自己目前生活状态的满意程度时,给出的区间内的一个数,该数越接近10表示越满意,为了解某大城市市民的幸福感,随机对该城市的男、女各500人市民进行了调查,调查数据如下表所示: