题目内容
14.若角α与角β的终边关于y轴对称,则( )| A. | α+β=π+kπ(k∈Z) | B. | α+β=π+2kπ(k∈Z) | C. | $α+β=\frac{π}{2}+kπ(k∈Z)$ | D. | $α+β=\frac{π}{2}+2kπ(k∈Z)$ |
分析 根据角α与角β的终边关于y轴对称,即可确定α与β的关系.
解答 解:∵π-α是与α关于y轴对称的一个角,
∴β与π-α的终边相同,
即β=2kπ+(π-α)
∴α+β=α+2kπ+(π-α)=(2k+1)π,
故答案为:α+β=(2k+1)π或α=-β+(2k+1)π,k∈z,
故选:B.
点评 本题主要考查角的对称之间的关系,根据终边相同的关系是解决本题的关键,比较基础.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
9.在平面xOy内,向图形x2+y2≤4内投点,则点落在由不等式组$\left\{\begin{array}{l}x-y≥0\\ x+y≥0\end{array}\right.$所确定的平面区域的概率为( )
| A. | $\frac{3}{4}$ | B. | $\frac{2}{5}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |
19.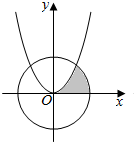 若(x2+$\frac{a}{2x}$)6展开式的常数项是15,图中阴影部分是由曲线y=x2和圆x2+y2=a及x轴围成的封闭图形,现向圆中投入一颗石子,则此石子恰好落在阴影部分的概率为( )
若(x2+$\frac{a}{2x}$)6展开式的常数项是15,图中阴影部分是由曲线y=x2和圆x2+y2=a及x轴围成的封闭图形,现向圆中投入一颗石子,则此石子恰好落在阴影部分的概率为( )
 若(x2+$\frac{a}{2x}$)6展开式的常数项是15,图中阴影部分是由曲线y=x2和圆x2+y2=a及x轴围成的封闭图形,现向圆中投入一颗石子,则此石子恰好落在阴影部分的概率为( )
若(x2+$\frac{a}{2x}$)6展开式的常数项是15,图中阴影部分是由曲线y=x2和圆x2+y2=a及x轴围成的封闭图形,现向圆中投入一颗石子,则此石子恰好落在阴影部分的概率为( )| A. | $\frac{1}{8}$-$\frac{1}{12π}$ | B. | $\frac{1}{8}$+$\frac{1}{12π}$ | C. | $\frac{1}{8}$ | D. | $\frac{1}{12π}$ |
6.根据表格中的数据,可以判定方程ex-x-2=0的一个根所在的区间为( )
| x | -1 | 0 | 1 | 2 | 3 |
| ex-x-2 | -0.63 | -1 | -0.28 | 3.39 | 15.09 |
| A. | (-1,0) | B. | (0,1) | C. | (1,2) | D. | (2,3) |
3.已知集合M={x|x>1},集合N{x|-3<x<2},则M∪N=( )
| A. | {x|-3<x<2} | B. | {x|-3<x<1} | C. | {x|1<x<2} | D. | {x|x>-3} |
4.设全集U=R,集合A={1,3,5,7},B={x|3<x<7},则A∩(∁UB)=( )
| A. | {1,3,5} | B. | {1,3,7} | C. | {5} | D. | {1} |