题目内容
9．设函数y=x3与y=2x+1的图象的交点为（x0，y0），则x0所在的区间是（ ）| A． | （0，1） | B． | （1，2） | C． | （2，3） | D． | （3，4） |
分析 由题意可得函数f（x）=x3 -（2x+1）的零点为x0．再利用函数零点的判定定理，得出结论．
解答 解：由于函数y=x3与y=2x+1的图象的交点为（x0，y0），
∵2x+1＞1，∴x3＞1，∴x0＞1．
函数f（x）=x3 -（2x+1）的零点为x0．
再根据f（1）=-1，f（2）=3，f（1）•f（2）＜0，故f（x）的零点为x0∈（1，2），
故选：B．
点评 本题主要考查函数的图象特征，函数零点的判定定理，属于基础题．
练习册系列答案
小学课时特训系列答案
相关题目
19．
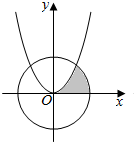若（x2+$\frac{a}{2x}$）6展开式的常数项是15，图中阴影部分是由曲线y=x2和圆x2+y2=a及x轴围成的封闭图形，现向圆中投入一颗石子，则此石子恰好落在阴影部分的概率为（ ）
若（x2+$\frac{a}{2x}$）6展开式的常数项是15，图中阴影部分是由曲线y=x2和圆x2+y2=a及x轴围成的封闭图形，现向圆中投入一颗石子，则此石子恰好落在阴影部分的概率为（ ）| A． | $\frac{1}{8}$-$\frac{1}{12π}$ | B． | $\frac{1}{8}$+$\frac{1}{12π}$ | C． | $\frac{1}{8}$ | D． | $\frac{1}{12π}$ |
4．设全集U=R，集合A={1，3，5，7}，B={x|3＜x＜7}，则A∩（∁UB）=（ ）
| A． | {1，3，5} | B． | {1，3，7} | C． | {5} | D． | {1} |