题目内容
7.圆x2+y2-2x+4y+1=0的半径为( )| A. | 1 | B. | $\sqrt{2}$ | C. | 2 | D. | 4 |
分析 将圆方程化为标准方程,找出半径即可.
解答 解:圆x2+y2-2x+4y+1=0变形得:(x-1)2+(y+2)2=4,
∴圆的半径为2.
故选:C.
点评 本题考查了圆的标准方程,将所求圆方程化为标准方程是解本题的关键,是基础题.

练习册系列答案
相关题目
15.用集合表示终边在阴影部分的角a的集合为( )
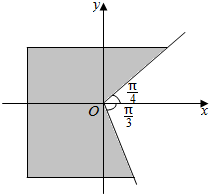

| A. | {a|$\frac{π}{4}$≤a≤$\frac{π}{3}$} | B. | {a|$\frac{π}{4}$≤a≤$\frac{5π}{3}$} | ||
| C. | {a|2kπ+$\frac{π}{4}$≤a≤2kπ+$\frac{π}{3}$,k∈Z} | D. | {a|2kπ+$\frac{π}{4}$≤a≤2kπ+$\frac{5π}{3}$,k∈Z} |
15.如图,在四面体ABCD中,设G是CD的中点,则$\overrightarrow{AB}+\frac{1}{2}(\overrightarrow{BD}+\overrightarrow{BC})$等于( )
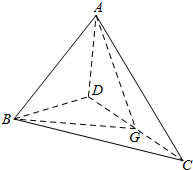

| A. | $\overrightarrow{AD}$ | B. | $\overrightarrow{BG}$ | C. | $\overrightarrow{CD}$ | D. | $\overrightarrow{AG}$ |
19.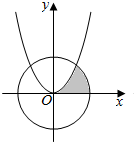 若(x2+$\frac{a}{2x}$)6展开式的常数项是15,图中阴影部分是由曲线y=x2和圆x2+y2=a及x轴围成的封闭图形,现向圆中投入一颗石子,则此石子恰好落在阴影部分的概率为( )
若(x2+$\frac{a}{2x}$)6展开式的常数项是15,图中阴影部分是由曲线y=x2和圆x2+y2=a及x轴围成的封闭图形,现向圆中投入一颗石子,则此石子恰好落在阴影部分的概率为( )
 若(x2+$\frac{a}{2x}$)6展开式的常数项是15,图中阴影部分是由曲线y=x2和圆x2+y2=a及x轴围成的封闭图形,现向圆中投入一颗石子,则此石子恰好落在阴影部分的概率为( )
若(x2+$\frac{a}{2x}$)6展开式的常数项是15,图中阴影部分是由曲线y=x2和圆x2+y2=a及x轴围成的封闭图形,现向圆中投入一颗石子,则此石子恰好落在阴影部分的概率为( )| A. | $\frac{1}{8}$-$\frac{1}{12π}$ | B. | $\frac{1}{8}$+$\frac{1}{12π}$ | C. | $\frac{1}{8}$ | D. | $\frac{1}{12π}$ |
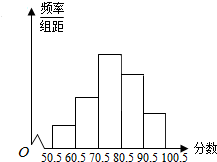 从全校参加数学竞赛的学生的试卷中,抽取一个样本,考察竞赛的成绩分布,将样本分成5组,绘成频率分布直方图,图中从左到右各小组的长方形的高之比为1:3:6:4:2,最右边一组的频数是6.
从全校参加数学竞赛的学生的试卷中,抽取一个样本,考察竞赛的成绩分布,将样本分成5组,绘成频率分布直方图,图中从左到右各小组的长方形的高之比为1:3:6:4:2,最右边一组的频数是6.