题目内容
9.已知函数f(x)=x2-(a+2)x+alnx,常数a>0(1)当x=1时,函数f(x)取得极小值-2,求函数f(x)的极大值
(2)设定义在D上的函数y=h(x)在点P(x0,h(x0))处的切线方程为l:y=g(x),当x≠x0时,若$\frac{h(x)-g(x)}{{x-{x_0}}}>0$在D内恒成立,则称点P为h(x)的“类优点”,若点(1,f(1))是函数f(x)的“类优点”,
①求函数f(x)在点(1,f(1))处的切线方程
②求实数a的取值范围.
分析 (1)求出函数的导数,解关于导函数的不等式,求出函数的单调区间,从而求出函数的极大值即可;
(2)①求出函数的导数,计算f(1),f′(1)的值,求出切线方程即可;
②结合题意得到F(x)=f(x)-g(x)=x2-(a+2)x+alnx+a+1,通过讨论a的范围得到函数的单调性,进而确定a的范围即可.
解答 解:(1)由题意,f(1)=1-(a+2)=-2,得a=1,
此时$f'(x)=2x-3+\frac{1}{x}=\frac{{({x-1})({2x-1})}}{x}$,(x>0)…(2分)
令f'(x)=0,得x=1或$x=\frac{1}{2}$…(3分)
当$0<x<\frac{1}{2}或x>1$时,f'(x)>0; 当$\frac{1}{2}<x<1$时,f'(x)<0
所以f(x)在$({0,\frac{1}{2}})$与(1,+∞)上单调递增,在$({\frac{1}{2},1})$上递减
所以当$x=\frac{1}{2}$时,f(x)有极大值$-\frac{5}{4}+ln\frac{1}{2}$…(4分)
(2)①∵$f'(x)=2x-({a+2})+\frac{a}{x}=\frac{{({2x-a})({x-1})}}{x}$,(x>0)
∴f(1)=1-(a+2)=-a-1,f'(1)=0
所以函数f(x)在点(1,f(1))处的切线方程为g(x)=-a-1…(6分)
②若点(1,f(1))是函数f(x)的“类优点”,
令F(x)=f(x)-g(x)=x2-(a+2)x+alnx+a+1常数a>0,
$则当x∈({0,1})∪({1,+∞})时,恒有\frac{F(x)}{x-1}>0$
又F(1)=0,且∵$F'(x)=2x-({a+2})+\frac{a}{x}=\frac{{({2x-a})({x-1})}}{x}$,(x>0)
令F'(x)=0,得x=1或$x=\frac{a}{2}$,a>0…(8分)
则当a=2时,∵F'(x)≥0,F(x)在(0,+∞)上递增
∴当x∈(0,1)时,F(x)<F(1)=0;
当x∈(1,+∞)时,F(x)>F(1)=0
故当x≠1时,恒有$\frac{F(x)}{x-1}>0$成立…(9分)
当a>2时,由F'(x)<0,得$1<x<\frac{a}{2}$,
∴F(x)在$({1,\frac{a}{2}})$上递减,F(x)<F(1)=0.
所以在,$1<x<\frac{a}{2}$,$\frac{F(x)}{x-1}>0$不成立.…(10分)
当0<a<2时,由F'(x)<0,得$\frac{a}{2}<x<1$,
∴F(x)在$({\frac{a}{2},1})$上递减,F(x)>F(1)=0.
所以在,$\frac{a}{2}<x<1$,$\frac{F(x)}{x-1}>0$不成立…(11分)
综上可知,若点(1,f(1))是函数f(x)的“类优点”,则实数a=2…(12分)
点评 本题考查了函数的单调性、极值问题,考查导数的应用以及分类讨论思想,考查新定义的理解,是一道中档题.

 一本好题口算题卡系列答案
一本好题口算题卡系列答案| A. | 命题“若lgx=0,则x=0”的逆否命题为“若x≠0,则lgx≠0” | |
| B. | 若p∧q为假命题,则p,q均为假命题 | |
| C. | 命题p:?x0∈R,使得sinx0>1,则¬p“?x∈R,均有sinx≤1 | |
| D. | “x>2”是“$\frac{1}{x}$<$\frac{1}{2}$”的充分不必要条件 |
| A. | {1,2} | B. | {2,3} | C. | {3,4} | D. | {4,5} |
| A. | $?{x_0}∈R,{x_0}^2+2>0$ | B. | $?{x_0}∈R,{x_0}^2+2≤0$ | ||
| C. | $?{x_0}∈R,{x_0}^2+2<0$ | D. | ?x∈R,x2+2≤0 |
| A. | 1 | B. | 3 | C. | $\frac{{5\sqrt{7}}}{7}$ | D. | $\frac{{15\sqrt{7}}}{7}$ |
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{5}{6}$ |
| A. | 4 | B. | 2 | C. | $\frac{1}{8}$ | D. | $\frac{1}{16}$ |
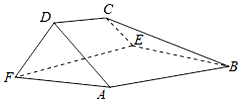 如图,在以A,B,C,D,E,F为顶点的五面体中,面ABEF为正方形,AF=2FD,∠AFD=90°,且二面角D-AF-E与二面角C-BE-F都是60°.
如图,在以A,B,C,D,E,F为顶点的五面体中,面ABEF为正方形,AF=2FD,∠AFD=90°,且二面角D-AF-E与二面角C-BE-F都是60°.