题目内容
函数f(x)=
是定义在(-∞,+∞)上的奇函数,且f(
)=
.
(1)求实数a,b,并确定函数f(x)的解析式;
(2)判断f(x)在(-1,1)上的单调性,并用定义证明你的结论;
(3)写出f(x)的单调减区间,并判断f(x)有无最大值或最小值?如有,写出最大值或最小值.(不需要说明理由)
| ax+b |
| x2+1 |
| 1 |
| 2 |
| 2 |
| 5 |
(1)求实数a,b,并确定函数f(x)的解析式;
(2)判断f(x)在(-1,1)上的单调性,并用定义证明你的结论;
(3)写出f(x)的单调减区间,并判断f(x)有无最大值或最小值?如有,写出最大值或最小值.(不需要说明理由)
考点:函数奇偶性的性质
专题:函数的性质及应用
分析:(1)根据奇函数的定义即可求得b=0,根据f(
)=
可求出a=1,所以便可求出f(x)的解析式;
(2)根据单调性的定义即可证明函数f(x)在(-1,1)上单调递增;
(3)根据基本不等式:a+b≥2
,a>0,b>0,所以分成x>0和x<0,从而用上基本不等式,并能求函数f(x)的最值.
| 1 |
| 2 |
| 2 |
| 5 |
(2)根据单调性的定义即可证明函数f(x)在(-1,1)上单调递增;
(3)根据基本不等式:a+b≥2
| ab |
解答:
解:(1)∵f(x)是奇函数;
∴f(-x)=-f(x),∴
=
,∴-ax+b=-ax-b,∴b=0;
∴f(x)=
,f(
)=
=
,∴a=1;
∴f(x)=
(2)设x1,x2∈(-1,1),且x1<x2则:
f(x1)-f(x2)=
-
=
=
;
∵-1<x1<x2<1,∴x1-x2<0,1-x1x2>0,∴f(x1)-f(x2)<0,即:f(x1)<f(x2);
∴f(x)在(-1,1)上是增函数;
(3)由(2)知,x1,x2∈(1,+∞)或(-∞,-1)时,x1-x2<0,1-x1x2<0,∴f(x1)>f(x2);
∴函数f(x)的单调减区间为(1,+∞),(-∞,-1);
x>0时,f(x)=
=
,∵x+
≥2,∴0<
≤
,∴函数f(x)的最大是
;
x<0时,f(x)=
=
=-
,-x>0,-x+
≥2,0<
≤
,-
≤-
<0,∴函数f(x)最小值是-
;
∴函数f(x)的最大值为
,最小值为-
.
∴f(-x)=-f(x),∴
| -ax+b |
| x2+1 |
| -ax-b |
| x2+1 |
∴f(x)=
| ax |
| x2+1 |
| 1 |
| 2 |
| ||
|
| 2 |
| 5 |
∴f(x)=
| x |
| x2+1 |
(2)设x1,x2∈(-1,1),且x1<x2则:
f(x1)-f(x2)=
| x1 |
| x12+1 |
| x2 |
| x22+1 |
| x1(x22+1)-(x12+1)x2 |
| (x12+1)(x22+1) |
| (x1-x2)(1-x1x2) |
| (x12+1)(x22+1) |
∵-1<x1<x2<1,∴x1-x2<0,1-x1x2>0,∴f(x1)-f(x2)<0,即:f(x1)<f(x2);
∴f(x)在(-1,1)上是增函数;
(3)由(2)知,x1,x2∈(1,+∞)或(-∞,-1)时,x1-x2<0,1-x1x2<0,∴f(x1)>f(x2);
∴函数f(x)的单调减区间为(1,+∞),(-∞,-1);
x>0时,f(x)=
| x |
| x2+1 |
| 1 | ||
x+
|
| 1 |
| x |
| 1 | ||
x+
|
| 1 |
| 2 |
| 1 |
| 2 |
x<0时,f(x)=
| x |
| x2+1 |
| 1 | ||
x+
|
| 1 | ||
-x+
|
| 1 |
| -x |
| 1 | ||
-x+
|
| 1 |
| 2 |
| 1 |
| 2 |
| 1 | ||
-x+
|
| 1 |
| 2 |
∴函数f(x)的最大值为
| 1 |
| 2 |
| 1 |
| 2 |
点评:考查奇函数的定义,单调性的定义,根据单调性的定义求单调区间,根据基本不等式求函数的最值.

练习册系列答案
相关题目
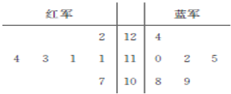 解放军某部在实兵演练对抗比赛中,红、蓝两个小组均派6人参加实弹射击,其所得成绩的茎叶图如图所示.
解放军某部在实兵演练对抗比赛中,红、蓝两个小组均派6人参加实弹射击,其所得成绩的茎叶图如图所示. 如图,某观测站C在城A的南偏西20°方向上,从城A出发有一条公路,走向是南偏东40°.在C处测得距离C为31千米的公路上的B处有一辆车正沿着公路向城A驶去.该车行驶了20千米后到达D处停下,此时测得C、D两处距离为21千米.
如图,某观测站C在城A的南偏西20°方向上,从城A出发有一条公路,走向是南偏东40°.在C处测得距离C为31千米的公路上的B处有一辆车正沿着公路向城A驶去.该车行驶了20千米后到达D处停下,此时测得C、D两处距离为21千米.