题目内容
4.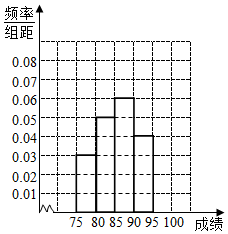 将某校高三年级300名学生的毕业会考数学成绩进行整理后,分成五组,第-组[75,80),第二组[80,85),第三组[86,90),第四组[90,95),第五组[95,100],如图为频率分布直方图的一部分.
将某校高三年级300名学生的毕业会考数学成绩进行整理后,分成五组,第-组[75,80),第二组[80,85),第三组[86,90),第四组[90,95),第五组[95,100],如图为频率分布直方图的一部分.(1)请在图中补全频率分布直方图并估算这300名学生数学成绩的中位数;
(2)若M大学决定在成绩高的第3,4,5组中用分层抽样的方法抽取6名学生进行面试,在这6名学生中随机抽取2名学生接受考官B的面试,求第4组中至少有1名学生被考官B面试的概率.
分析 (1)根据频率和为1,求出第五组的频率和$\frac{频率}{组距}$,补全频率分布直方图即可;
根据中位数两边频率相等,求出中位数的值;
(2)计算用分层抽样法从第3、4、5组抽取6人时每组应抽取的人数,
利用列举法求出基本事件数与对应的概率值.
解答  解:(1)根据频率和为1,计算第五组[95,100]的频率为1-0.03×5-0.05×5-0.06×5-0.04×5=0.1,
解:(1)根据频率和为1,计算第五组[95,100]的频率为1-0.03×5-0.05×5-0.06×5-0.04×5=0.1,
又$\frac{频率}{组距}$=$\frac{0.1}{5}$=0.02,
补全频率分布直方图如图所示
∵0.03×5+0.05×5=0.40<0.5,
0.40+0.06×5=0.70>0.5,
∴中位数在第三组[85,90)中,设为x,
则(x-85)×5+0.40=0.50,
解得x=87;
估算这300名学生数学成绩的中位数87;
(2)第3组有学生300×0.06×5=90人,第4组有学生300×0.04×5=60人,
第5组有学生300×0.02×5=30人;
用分层抽样的方法从中抽取6人,则第3组抽取3人,记为a、b、c,
第4组抽取2人,记为D、E,第5组抽取1人,记为f;
从这6名学生中随机抽取2人,基本事件为
ab、ac、aD、aE、af、bc、bD、bE、bf、cD、cE、cf、DE、Df、Ef共15种,
第4组中至少有1人被抽取的基本事件为
aD、aE、bD、bE、cD、cE、DE、Df、Ef共9种,
故所求的概率为P=$\frac{9}{15}$=$\frac{3}{5}$.
点评 本题考查了频率分布直方图的应用问题,也考查了用列举法求古典概型的概率问题,是基础题目.

练习册系列答案
相关题目
12.已知函数f(x)=x2-x+lnx的图象在点P(x0,y0)处的切线方程为y=g(x),若不等式$\frac{f(x)-g(x)}{x-{x}_{0}}$>0对任意x∈(0,x0)∪(x0,+∞)恒成立,则x0=( )
| A. | 1 | B. | $\frac{\sqrt{2}}{2}$ | C. | 2 | D. | $\sqrt{2}$ |
9.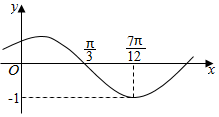 已知函数f(x)=Asin(ωx+φ)(其中A>0,|φ|<$\frac{π}{2}$)的图象如图所示,将函数f(x)的图象向左平移$\frac{π}{6}$个单位长度得到函数g(x)的图象,则函数g(x)的解析式为( )
已知函数f(x)=Asin(ωx+φ)(其中A>0,|φ|<$\frac{π}{2}$)的图象如图所示,将函数f(x)的图象向左平移$\frac{π}{6}$个单位长度得到函数g(x)的图象,则函数g(x)的解析式为( )
 已知函数f(x)=Asin(ωx+φ)(其中A>0,|φ|<$\frac{π}{2}$)的图象如图所示,将函数f(x)的图象向左平移$\frac{π}{6}$个单位长度得到函数g(x)的图象,则函数g(x)的解析式为( )
已知函数f(x)=Asin(ωx+φ)(其中A>0,|φ|<$\frac{π}{2}$)的图象如图所示,将函数f(x)的图象向左平移$\frac{π}{6}$个单位长度得到函数g(x)的图象,则函数g(x)的解析式为( )| A. | g(x)=sin(2x-$\frac{π}{3}$) | B. | g(x)=sin(2x+$\frac{π}{6}$) | C. | g(x)=-sin(2x-$\frac{π}{3}$) | D. | g(x)=sin(4x+$\frac{π}{6}$) |
12.直线y-4=-$\sqrt{3}$(x+3)的倾斜角和所过的定点分别是( )
| A. | -60°,(-3,4) | B. | 120°,(-3,4) | C. | 150°,(-3,4) | D. | 120°,(3,-4) |
9.函数f(x)=Acos(ωx+φ)(A>0,ω>0)在x=2015处取得最小值,则( )
| A. | f(x-2015)一定是奇函数 | B. | f(x-2015)一定是偶函数 | ||
| C. | f(x+2015)一定是奇函数 | D. | f(x+2015)一定是偶函数 |